题目内容
圆心角为
的扇形与其内切圆面积之比为（ ）
| π |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点：弧度制的应用
专题：计算题,三角函数的求值
分析：设圆的半径为r，则扇形的半径为3r，求出面积，即可得出结论．
解答：
解：设圆的半径为r，
∵圆心角为
，扇形的内切圆的圆心在圆心角的角平分线上，
∴扇形的半径为2r+r=3r，
∴圆心角为
的扇形与其内切圆面积之比为
=
，
故选A．
解：设圆的半径为r，∵圆心角为
| π |
| 3 |
∴扇形的半径为2r+r=3r，
∴圆心角为
| π |
| 3 |
| ||||
| πr2 |
| 3 |
| 2 |
故选A．
点评：本题考查了扇形的面积公式，解决本题的难点是得到扇形的内切圆半径和扇形半径的关系．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
已知实数x＞0，y＞0，0＜λ＜2，且x+y=3，则
+
+
的最小值为（ ）
| 1 |
| x |
| 2 |
| (2-λ)y |
| 2 |
| λy |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
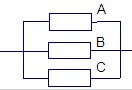如图，在一段线路中并联着3个自动控制的开关，只要其中有一个开关能够闭合，线路就正常工作，假在某段时间内每个开关能够闭合的概率是0.5，请你用树状图求出在这段时间内正常工作的概率．已知0＜t≤
，那么
-t的最小值是（ ）
| 1 |
| 4 |
| 1 |
| t |
A、
| ||
B、
| ||
| C、2 | ||
| D、-2 |