题目内容
已知实数x>0,y>0,0<λ<2,且x+y=3,则
+
+
的最小值为( )
| 1 |
| x |
| 2 |
| (2-λ)y |
| 2 |
| λy |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
考点:基本不等式
专题:不等式的解法及应用
分析:由于实数x>0,y>0,x+y=3,可得2x+(2-λ)y+λy=6.变形为∴
+
+
=
[2x+(2-λ)y+λy][
+
+
],利用基本不等式的性质即可得出.
| 1 |
| x |
| 2 |
| (2-λ)y |
| 2 |
| λy |
| 1 |
| 6 |
| 2 |
| 2x |
| 2 |
| (2-λ)y |
| 2 |
| λy |
解答:
解:∵实数x>0,y>0,x+y=3,
∴2x+(2-λ)y+λy=6.
∴
+
+
=
[2x+(2-λ)y+λy][
+
+
]
≥
•3
•3
=3,
当且仅当2x=(2-λ)y=λy,x+y=3,即x=1,y=2,λ=1时取等号.
∴
+
+
的最小值为3.
故选:D.
∴2x+(2-λ)y+λy=6.
∴
| 1 |
| x |
| 2 |
| (2-λ)y |
| 2 |
| λy |
| 1 |
| 6 |
| 2 |
| 2x |
| 2 |
| (2-λ)y |
| 2 |
| λy |
≥
| 1 |
| 3 |
| 3 | 2x•(2-λ)y•λy |
| 3 |
| ||||||
当且仅当2x=(2-λ)y=λy,x+y=3,即x=1,y=2,λ=1时取等号.
∴
| 1 |
| x |
| 2 |
| (2-λ)y |
| 2 |
| λy |
故选:D.
点评:本题考查了变形利用基本不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
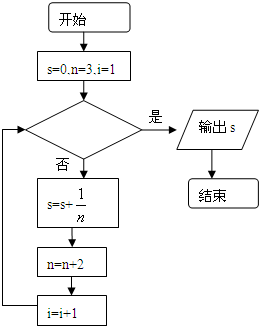
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 21 |

| A、i>10? |
| B、i<10? |
| C、i>20? |
| D、i<20? |
设x,y满足约束条件
,若目标函数z=abx+y(a>0,b>0)的最大值为8,则(a2+b2)-10(a+b)的最小值为( )
|
| A、-32 | B、-33 |
| C、-34 | D、-35 |
圆心角为
的扇形与其内切圆面积之比为( )
| π |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |