题目内容
已知0＜t≤
，那么
-t的最小值是（ ）
| 1 |
| 4 |
| 1 |
| t |
A、
| ||
B、
| ||
| C、2 | ||
| D、-2 |
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：先判断函数的单调性，由单调性再求函数的最小值．
解答：
解：令f（x）=
-x，∵y=
和y=-x在区（0，
]上都是单调递减间，∴函数f（x）在（0，
]上单调递减，
∴当x=
时，有最小值f（
）=
．
故答案选择：A．
| 1 |
| x |
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 4 |
∴当x=
| 1 |
| 4 |
| 1 |
| 4 |
| 15 |
| 4 |
故答案选择：A．
点评：本题考查函数在闭区上的最值．由单调性即可以求出最值．属于基础题．
练习册系列答案
相关题目
圆心角为
的扇形与其内切圆面积之比为（ ）
| π |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
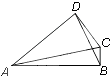如图，在四边形ABCD中，AB⊥BC，AD⊥DC．若| AB |
| a |
| AD |
. |
| b |
| AC |
| BD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知an=
，则这个数列的前100项中最大项和最小项分别是（ ）
| ||
|
| A、a1，a100 |
| B、a100，a1 |
| C、a45，a44 |
| D、a45，a46 |
实数x，y满足