题目内容
已知关于x的不等式|x+1|+|2x-1|<|m-1|+|m-2|有解,求m的取值范围.
考点:绝对值不等式的解法
专题:计算题,分类讨论,不等式的解法及应用
分析:令f(x)=|x+1|+|2x-1|,分当x≥
时,当-1<x<
时,当x≤-1时,求得函数的值域,得到最小值,再对当m≥2时,当1<m<2时,当m≤1时,求出m的范围,最后再求并集即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:令f(x)=|x+1|+|2x-1|,
当x≥
时,f(x)=x+1+2x-1=3x,且f(x)≥
;
当-1<x<
时,f(x)=x+1+1-2x=2-x,且
<f(x)<3;
当x≤-1时,f(x)=-x-1+1-2x=-3x,且f(x)≥3.
则有f(x)的值域为:[
,+∞).
由于关于x的不等式|x+1|+|2x-1|<|m-1|+|m-2|有解,
则|m-1|+|m-2|>
,
当m≥2时,m-1+m-2>
,解得m>
,即有m>
;
当1<m<2时,m-1+2-m>
,则m无解;
当m≤1时,1-m+2-m>
,解得m<
,即有m<
.
综上可得,m的取值范围是:(
,+∞)∪(-∞,
).
当x≥
| 1 |
| 2 |
| 3 |
| 2 |
当-1<x<
| 1 |
| 2 |
| 3 |
| 2 |
当x≤-1时,f(x)=-x-1+1-2x=-3x,且f(x)≥3.
则有f(x)的值域为:[
| 3 |
| 2 |
由于关于x的不等式|x+1|+|2x-1|<|m-1|+|m-2|有解,
则|m-1|+|m-2|>
| 3 |
| 2 |
当m≥2时,m-1+m-2>
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
当1<m<2时,m-1+2-m>
| 3 |
| 2 |
当m≤1时,1-m+2-m>
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
综上可得,m的取值范围是:(
| 9 |
| 4 |
| 3 |
| 4 |
点评:本题考查绝对值不等式的解法,考查含绝对值函数的最值问题,注意分类讨论的思想方法,考查运算能力,属于中档题.

练习册系列答案
相关题目
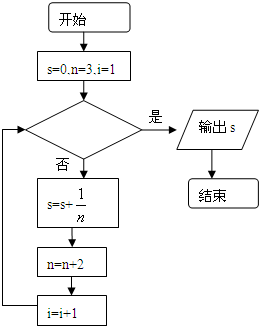
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 21 |

| A、i>10? |
| B、i<10? |
| C、i>20? |
| D、i<20? |
从区间[-1,4]上随机取一个数x,则x∈[0,2]的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(x)=ax3+bx-4,若f(-2)=2,则f(2)=( )
| A、-2 | B、-4 | C、-6 | D、-10 |
圆心角为
的扇形与其内切圆面积之比为( )
| π |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
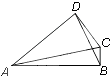 如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若
如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若| AB |
| a |
| AD |
. |
| b |
| AC |
| BD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 实数x,y满足
实数x,y满足