题目内容
函数y=lg(ax+1)在(-∞,1)上单调递减,求a的取值范围.
考点:复合函数的单调性
专题:函数的性质及应用
分析:题目给出的函数是复合函数,外层函数对数函数是增函数,要使复合函数在(-∞,1)上单调递减,需要内层函数在(-∞,1)上单调递减,可知a>0,同时保证在x=1时,ax+1大于等于0,由此列不等式组求解a的取值范围.
解答:
解:令t=ax+1,则原函数化为g(t)=lgt,
外层函数g(t)=lgt为增函数,
要使复合函数f(x)=lg(ax+1)在(-∞,1)上单调递减,
则内层函数t=ax+1在(-∞,1)上单调递减,且
t=ax+1在(-∞,1)上大于0恒成立.
∴
,
解得:-1≤a<0.
∴使函数y=lg(ax+1)在(-∞,1)上单调递减的a的取值范围是[-1,0).
外层函数g(t)=lgt为增函数,
要使复合函数f(x)=lg(ax+1)在(-∞,1)上单调递减,
则内层函数t=ax+1在(-∞,1)上单调递减,且
t=ax+1在(-∞,1)上大于0恒成立.
∴
|
解得:-1≤a<0.
∴使函数y=lg(ax+1)在(-∞,1)上单调递减的a的取值范围是[-1,0).
点评:本题考查了复合函数的单调性,考查了数学转化思想方法,内层函数为减函数,把ax+1在(-∞,1)上恒大与0转化为当x=1时ax+1大于等于0.此题是中档题.

练习册系列答案
相关题目
设x,y满足约束条件
,若目标函数z=abx+y(a>0,b>0)的最大值为8,则(a2+b2)-10(a+b)的最小值为( )
|
| A、-32 | B、-33 |
| C、-34 | D、-35 |
从区间[-1,4]上随机取一个数x,则x∈[0,2]的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
圆心角为
的扇形与其内切圆面积之比为( )
| π |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
已知F1、F2分别是双曲线
-
=1(a>0,b>0)的左、右焦点,过点F1且斜率为k的直线与双曲线的右支交于点M,若点M在x轴上的射影恰好是右焦点F2,且
<k<
,则双曲线离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
| 4 |
| 3 |
| A、(1,2) |
| B、(1,3) |
| C、(3,+∞) |
| D、(2,3) |
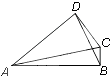 如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若
如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若| AB |
| a |
| AD |
. |
| b |
| AC |
| BD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
