题目内容
15.已知函数f(x)=xln x-a(x-1),其中a∈R,求函数f(x)在区间[1,e]上的最小值.分析 求出函数f(x)的导数,通过讨论a的范围,求出函数f(x)的单调区间,从而求出函数f(x)在[1,e]的最小值即可.
解答 解:f'(x)=lnx+1-a,令f'(x)=0,∴x=ea-1,
∴f(x)在区间(0,ea-1)单调递减,在区间(ea-1,+∞)单调递增,
∴f(x)min=f(1)=0;
当ea-1≤1即a≤1时,f(x)在区间[1,e]上单调递增,
1<ea-1<e即1<a<2时,f(x)在[1,ea-1)递减,在(ea-1,e]递增,
∴$f{(x)_{min}}=f({e^{a-1}})=a-{e^{a-1}}$,
当ea-1≥e即a≥2时,f(x)在[1,e]递减,
∴f(x)min=f(e)=a+e-ae,
综上:当a≤1时,f(x)的最小值为0,
当1<a<2时,f(x)的最小值为a-ea-1;
当a≥2时,f(x)的最小值为a+e-ae.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
5.函数y=sin(x-$\frac{π}{4}$)cos(x+$\frac{π}{4}$)+$\frac{1}{2}$是( )
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为π的偶函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的奇函数 | D. | 最小正周期为$\frac{π}{2}$的偶函数 |
6.已知-$\frac{π}{6}$<α<$\frac{π}{6}$,且cos(α+$\frac{π}{6}$)=$\frac{4}{5}$,则sin(2α+$\frac{π}{12}$)的值为( )
| A. | $\frac{17\sqrt{2}}{50}$ | B. | $\frac{31\sqrt{2}}{50}$ | C. | $\frac{7\sqrt{2}}{10}$ | D. | $\frac{\sqrt{2}}{10}$ |
3.点P在曲线y=x3-x+7上移动,过点P的切线倾斜角的取值范围是( )
| A. | [0,π] | B. | $[0,\frac{π}{2})∪[\frac{3π}{4},π)$ | C. | $[0,\frac{π}{2})∪[\frac{π}{2},π)$ | D. | $[0,\frac{π}{2}]∪[\frac{3π}{4},π)$ |
20.已知α∈[$\frac{π}{2}$,$\frac{3π}{2}$],β∈[-$\frac{π}{2}$,0],且(α-$\frac{π}{2}$)3-sinα-2=0,8β3+2cos2β+1=0,则sin($\frac{α}{2}$+β)的值为( )
| A. | 0 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
4.已知函数f(x)=-x2+2lnx的极大值是函数g(x)=x+$\frac{a}{x}$的极小值的-$\frac{1}{2}$倍,并且$?{x_1},{x_2}∈[\frac{1}{e},3]$,不等式$\frac{{f({x_1})-g({x_2})}}{k-1}$≤1恒成立,则实数k的取值范围是( )
| A. | $(-∞,-\frac{40}{3}+2ln3]∪(-1,1)∪(1,+∞)$ | B. | $(-∞,-\frac{34}{3}+2ln3]∪(1,+∞)$ | ||
| C. | $(-∞,-\frac{34}{3}+2ln3]∪[-1,1)∪(1,+∞)$ | D. | $(-∞,-\frac{40}{3}+2ln3]∪(1,+∞)$ |
5.已知函数y=f(x)(x∈R)的图象如图所示,则不等式x•f(x)<0的解集为( )
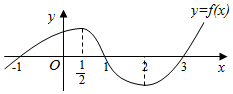

| A. | $(-∞,\frac{1}{2})∪(\frac{1}{2},2)$ | B. | (-1,0)∪(1,3) | C. | $(-∞,\frac{1}{2})∪(\frac{1}{2},+∞)$ | D. | $(-∞,\frac{1}{2})∪(2,+∞)$ |