题目内容
11.设a>1,若仅有一个常数c使得对于任意的x∈[a,3a]都有y∈[a,a3]满足方程logax+logay=c,则a的取值组成的集合为{3}.分析 由已知得y=$\frac{{a}^{c}}{x}$,单调递减,从而得到$\left\{\begin{array}{l}{\frac{{a}^{c}-1}{3}≥a}\\{{a}^{c-1}≤{a}^{3}}\end{array}\right.$,由此能求出a的取值的集合.
解答 解:∵logax+logay=c,
∴loga(xy)=c,∴xy=ac,
解得y=$\frac{{a}^{c}}{x}$,单调递减,
∴当x∈[a,3a]时,y∈[$\frac{{a}^{c}-1}{3}$,ac-1],
∴$\left\{\begin{array}{l}{\frac{{a}^{c}-1}{3}≥a}\\{{a}^{c-1}≤{a}^{3}}\end{array}\right.$,∴$\left\{\begin{array}{l}{c≥3+lo{g}_{a}3}\\{c≤4}\end{array}\right.$,
∵有且只有一个常数c符合题意,∴3+loga3=4,
解得a=3,∴a的取值的集合为{3}.
故答案为:{3}.
点评 本题考查实数的取值集合的求法,是基础题,解题时要认真审题,注意对数性质、运算法则的合理运用.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
4.已知函数f(x)=-x2+2lnx的极大值是函数g(x)=x+$\frac{a}{x}$的极小值的-$\frac{1}{2}$倍,并且$?{x_1},{x_2}∈[\frac{1}{e},3]$,不等式$\frac{{f({x_1})-g({x_2})}}{k-1}$≤1恒成立,则实数k的取值范围是( )
| A. | $(-∞,-\frac{40}{3}+2ln3]∪(-1,1)∪(1,+∞)$ | B. | $(-∞,-\frac{34}{3}+2ln3]∪(1,+∞)$ | ||
| C. | $(-∞,-\frac{34}{3}+2ln3]∪[-1,1)∪(1,+∞)$ | D. | $(-∞,-\frac{40}{3}+2ln3]∪(1,+∞)$ |
5.已知函数y=f(x)(x∈R)的图象如图所示,则不等式x•f(x)<0的解集为( )
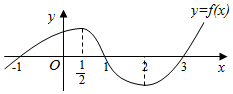

| A. | $(-∞,\frac{1}{2})∪(\frac{1}{2},2)$ | B. | (-1,0)∪(1,3) | C. | $(-∞,\frac{1}{2})∪(\frac{1}{2},+∞)$ | D. | $(-∞,\frac{1}{2})∪(2,+∞)$ |
6.已知a>0,则下列不等关系不恒成立的是( )
| A. | 若m>n,则$\frac{n+a}{m+a}$<$\frac{n}{m}$ | B. | a+$\frac{9}{a+2}$≥4 | ||
| C. | a2+$\frac{1}{{a}^{2}}$≥a+$\frac{1}{a}$ | D. | 若函数f(x)=|1-x2|,则f(ax)-a2f(x)≤f(a) |
16.已知等比数列{an}中,a1•a9=64,a3+a7=20,则a35=( )
| A. | 49 | B. | $\frac{1}{{4}^{6}}$ | C. | $\frac{1}{{4}^{6}}$或49 | D. | -49 |
1.已知点A(1,3),B(4,-1),则与向量$\overrightarrow{AB}$反方向的单位向量的坐标为( )
| A. | $(\frac{3}{5},-\frac{4}{5})$ | B. | $(\frac{4}{5},\frac{3}{5})$ | C. | $(-\frac{3}{5},\frac{4}{5})$ | D. | $(-\frac{4}{5},\frac{3}{5})$ |
