题目内容
20．若一扇形的圆心角为2，圆心角所对的弦长为2，则此扇形的面积为$\frac{1}{si{n}^{2}1}$．分析 根据扇形的面积公式直接计算即可．
解答 
解：∵弧度是2的圆心角所对的弦长为2，
∴半径OB=$\frac{1}{sin1}$．
∴扇形的面积公式S=$\frac{1}{2}×O{B}^{2}×2$=$\frac{1}{si{n}^{2}1}$，
故答案为：$\frac{1}{si{n}^{2}1}$．
点评 本题主要考查扇形的半径的求法、面积的求法，考查计算能力，注意扇形面积公式的应用．比较基础．
练习册系列答案
一线名师提优试卷系列答案
相关题目
5．已知函数y=f（x）（x∈R）的图象如图所示，则不等式x•f（x）＜0的解集为（ ）
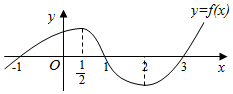
| A． | $（-∞，\frac{1}{2}）∪（\frac{1}{2}，2）$ | B． | （-1，0）∪（1，3） | C． | $（-∞，\frac{1}{2}）∪（\frac{1}{2}，+∞）$ | D． | $（-∞，\frac{1}{2}）∪（2，+∞）$ |
6．已知a＞0，则下列不等关系不恒成立的是（ ）
| A． | 若m＞n，则$\frac{n+a}{m+a}$＜$\frac{n}{m}$ | B． | a+$\frac{9}{a+2}$≥4 | ||
| C． | a2+$\frac{1}{{a}^{2}}$≥a+$\frac{1}{a}$ | D． | 若函数f（x）=|1-x2|，则f（ax）-a2f（x）≤f（a） |