题目内容
16．若α是第三象限角，则下列各式中不成立的是（ ）| A． | sin α+cos α＜0 | B． | tan α-sin α＜0 | C． | cos α-tan α＜0 | D． | tan αsin α＜0 |
分析 根据三角函数在不同象限的符号直接判断即可．
解答 解：由题意，α是第三象限角，sin α＜0，cos α＜0．tanα＞0，
由此判断：tan α-sin α＜0，一定不成立．
故选B．
点评 本题考查了三角函数在不同象限的符号判断，比较基础．
练习册系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
高效智能课时作业系列答案
相关题目
6．已知-$\frac{π}{6}$＜α＜$\frac{π}{6}$，且cos（α+$\frac{π}{6}$）=$\frac{4}{5}$，则sin（2α+$\frac{π}{12}$）的值为（ ）
| A． | $\frac{17\sqrt{2}}{50}$ | B． | $\frac{31\sqrt{2}}{50}$ | C． | $\frac{7\sqrt{2}}{10}$ | D． | $\frac{\sqrt{2}}{10}$ |
4．已知函数f（x）=-x2+2lnx的极大值是函数g（x）=x+$\frac{a}{x}$的极小值的-$\frac{1}{2}$倍，并且$?{x_1}，{x_2}∈[\frac{1}{e}，3]$，不等式$\frac{{f（{x_1}）-g（{x_2}）}}{k-1}$≤1恒成立，则实数k的取值范围是（ ）
| A． | $（-∞，-\frac{40}{3}+2ln3]∪（-1，1）∪（1，+∞）$ | B． | $（-∞，-\frac{34}{3}+2ln3]∪（1，+∞）$ | ||
| C． | $（-∞，-\frac{34}{3}+2ln3]∪[-1，1）∪（1，+∞）$ | D． | $（-∞，-\frac{40}{3}+2ln3]∪（1，+∞）$ |
1．已知函数f（x）=ax+elnx与g（x）=$\frac{{x}^{2}}{x-elnx}$的图象有三个不同的公共点，其中e为自然对数的底数，则实数a的取值范围为（ ）
| A． | a＜-e | B． | a＞1 | C． | a＞e | D． | a＜-3或a＞1 |
5．已知函数y=f（x）（x∈R）的图象如图所示，则不等式x•f（x）＜0的解集为（ ）
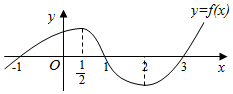
| A． | $（-∞，\frac{1}{2}）∪（\frac{1}{2}，2）$ | B． | （-1，0）∪（1，3） | C． | $（-∞，\frac{1}{2}）∪（\frac{1}{2}，+∞）$ | D． | $（-∞，\frac{1}{2}）∪（2，+∞）$ |