题目内容
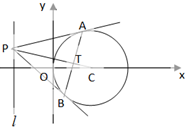已知圆C：（x-2）2+y2=4，从直线l：x=-2上一动点P引圆C的两条切线，切点分别为A，B，PC交AB于T．（1）求点T的轨迹方程；
（2）求S△ABC的最大值．
考点：圆方程的综合应用
专题：综合题,直线与圆
分析：（1）求出公共弦AB的方程、直线PC的方程，可得T的坐标，消去参数，即可求点T的轨迹方程；
（2）S△ABC=
AB•d，再求S△ABC的最大值．
（2）S△ABC=
| 1 |
| 2 |
解答：
解：（1）圆（x-2）2+y2=4的圆心为C（2，0），半径为2，
以P（-2，b）、C（2，0）为直径的圆的方程为x2+（y-
）2=
，
将两圆的方程相减可得公共弦AB的方程4x-by-4=0，
直线PC的方程为
=
由以上两个方程解得，x=
，y=
，
消去b可得x2+y2-3x+2=0（在圆C内部）；
（2）圆心C（2，0）到AB的距离为d=
，
∴AB=2
，
∴S△ABC=
AB•d=
，
令
=t（t≥4
），S△ABC=
=
≤
，
当且仅当t=4
，即b=0时，S△ABC的最大值为
．
以P（-2，b）、C（2，0）为直径的圆的方程为x2+（y-
| b |
| 2 |
| b2+16 |
| 4 |
将两圆的方程相减可得公共弦AB的方程4x-by-4=0，
直线PC的方程为
| y |
| b |
| x-2 |
| -2-2 |
由以上两个方程解得，x=
| 2b2+16 |
| b2+16 |
| 4b |
| b2+16 |
消去b可得x2+y2-3x+2=0（在圆C内部）；
（2）圆心C（2，0）到AB的距离为d=
| 4 | ||
|
∴AB=2
4-
|
∴S△ABC=
| 1 |
| 2 |
4
| ||
| 16+b2 |
令
| 48+b2 |
| 3 |
| 4t |
| t2-32 |
| 4 | ||
t-
|
| 3 |
当且仅当t=4
| 3 |
| 3 |
点评：本题考查圆的方程，考查直线与圆的位置关系，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=
，则下列结论正确的是（ ）
|
| A、f（x）是偶函数 |
| B、f（x）是增函数 |
| C、f（x）的值域为[-1，+∞） |
| D、f（x）是周期函数 |
若在甲袋内装有8个白球，4个红球，在乙袋内装有6个白球，6个红球，今从两袋里面各任意取出1个球，设取去的白球的个数为ξ，则下列概率中等于
的是（ ）
| ||||||||
|
| A、P（ξ=0） |
| B、P（ξ≤2） |
| C、P（ξ=1） |
| D、P（ξ=2） |
在正方形ABCD-A1B1C1D1中，G，H分别是B1C1，C1D1的中点．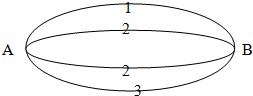
如图A、B两点之间有4条网线并联，他们能通过的最大信息量分别为1、2、2、3，现从中任取三条网线且使每条网线通过最大信息量；