题目内容
已知f(x)对于任意实数x,y满足f(x+y)=f(x)+f(y),当x>0时,f(x)>0.
(1)求f(0)并判断f(x)的奇偶性;
(2)判断f(x)的单调性,并用定义加以证明.
(1)求f(0)并判断f(x)的奇偶性;
(2)判断f(x)的单调性,并用定义加以证明.
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)首先令x=y=0,得f(0)=f(0)+f(0),解得f(0);然后令y=-x,得f(0)=f(x)+f(-x)=0,从而判断f(-)与f(x)的关系;
(2)设x1,x2∈R,x1<x2,利用f(x+y)=f(x)+f(y),将f(x2)-f(x1)=f[x1+(x2-x1)]-f(x1)变形,从而得到f(x2)-f(x1)与0的关系.
(2)设x1,x2∈R,x1<x2,利用f(x+y)=f(x)+f(y),将f(x2)-f(x1)=f[x1+(x2-x1)]-f(x1)变形,从而得到f(x2)-f(x1)与0的关系.
解答:
解:(1)令x=y=0,得f(0)=f(0)+f(0),∴f(0)=0
令y=-x,得f(0)=f(x)+f(-x)=0,
∴f(x)=-f(-x),
∴f(x)是奇函数…6分
(2)函数f(x)在R上是增函数.
证明如下:
设x1,x2∈R,x1<x2,
∴x2-x1>0,
由已知可得f(x2-x1)>0,
∴f(x2)-f(x1)=f[x1+(x2-x1)]-f(x1)=f(x1)+f(x2-x1)-f(x1)=f(x2-x1)>0
(或由(1)得f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1)>0)
∴f(x)在R上是增函数.…14分.
令y=-x,得f(0)=f(x)+f(-x)=0,
∴f(x)=-f(-x),
∴f(x)是奇函数…6分
(2)函数f(x)在R上是增函数.
证明如下:
设x1,x2∈R,x1<x2,
∴x2-x1>0,
由已知可得f(x2-x1)>0,
∴f(x2)-f(x1)=f[x1+(x2-x1)]-f(x1)=f(x1)+f(x2-x1)-f(x1)=f(x2-x1)>0
(或由(1)得f(x2)-f(x1)=f(x2)+f(-x1)=f(x2-x1)>0)
∴f(x)在R上是增函数.…14分.
点评:本题考查了函数的奇偶性的判断以及单调性的证明;对于抽象函数的奇偶性的判断要充分利用抽象函数的等式,常用适当地赋值判断f(-x)与f(x)的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某程序框图如右图所示,则输出的n值是( )


| A、.21 | B、22 |
| C、.23 | D、.24 |
设集合A={-1,0,1,2},B={-1,2,3},则A∩B=( )
| A、{-1,0,1,2,3} |
| B、{-1,2} |
| C、{0,1,3} |
| D、{x|-1≤x≤2} |
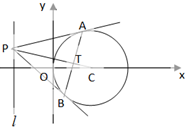 已知圆C:(x-2)2+y2=4,从直线l:x=-2上一动点P引圆C的两条切线,切点分别为A,B,PC交AB于T.
已知圆C:(x-2)2+y2=4,从直线l:x=-2上一动点P引圆C的两条切线,切点分别为A,B,PC交AB于T.