题目内容

在正方形ABCD-A1B1C1D1中，G，H分别是B1C1，C1D1的中点．
（1）画出平面ACD1与平面BDC1的交线，并说明理由；
（2）求证：B，D，H，G四点在同一平面内．
考点：平面的基本性质及推论
专题：综合题,空间位置关系与距离
分析：（1）利用平面基本性质2，可得结论；
（2）利用平面基本性质3，可得结论．
解答： （1）解：设AC∩BD=M，C1D∩CD1=N，连结MN，则
∵M，N分别在平面ACD1、平面BDC1，
∴平面ACD1∩平面BDC1=MN；
（2）证明：连B1D1，则HG∥D1B1∥DB．
故B、D、G、H四点共面
点评：本题考查平面基本性质，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知复数z1=cos2x+λi，z2=m+（sin2x-
3
m）i（λ，m，x∈R），且z1=z2．
（Ⅰ）若λ=0时，且
π
2
＜x＜π，求x的值；
（Ⅱ）设λ=f（x），求f（x）的单调递增区间．
设复数z1=3+i，z2=m-2i（m∈R），若z1•z2为实数，则m的值为
 
．
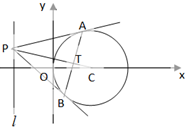已知圆C：（x-2）2+y2=4，从直线l：x=-2上一动点P引圆C的两条切线，切点分别为A，B，PC交AB于T．
（1）求点T的轨迹方程；
（2）求S△ABC的最大值．
已知f（x）=2mx2-2（4-m）x+1，g（x）=mx，若同时满足条件：
①?x∈R，f（x）＞0或g（x）＞0；
②?x∈（-∞，-4），f（x）g（x）＜0．
则实数m的取值范围是
 
．
已知△ABC中，已知cosA=-
1
3
，cosC=
2
sinB．
（1）求sinC的值．
（2）若a=
2
，求△ABC的面积．
甲、乙、丙、丁、戊5人随机站成一排，则甲、乙相邻，甲、丙不相邻的概率是
 
．
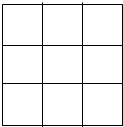将大小形状相同的4个红球和2个白球放入如图所示的九宫格中，每格至多放一个，要求相邻方格的小球不同色（有公共边的两个方格为相邻），则所有不同的放法种数为（　　）
A、32B、48C、50D、54
已知函数f（x）=x2+
a
x
（x≠0，a∈R），若函数f（x）在x∈[3，+∞）上是增函数，求a的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网