题目内容
已知函数f（x）=
，则下列结论正确的是（ ）
|
| A、f（x）是偶函数 |
| B、f（x）是增函数 |
| C、f（x）的值域为[-1，+∞） |
| D、f（x）是周期函数 |
考点：分段函数的应用
专题：阅读型,函数的性质及应用
分析：由三角函数和二次函数的性质，结合函数的奇偶性、单调性和周期性，及值域，分别对各个选项判断，可得A，B，D错，C正确．
解答：
解：由解析式可知当x≤0时，f（x）=cosx为周期函数，
当x＞0时，f（x）=x2+1，为二次函数的一部分，
故f（x）不是单调函数，不是周期函数，也不具备奇偶性，
故可排除A、B、D，
对于C，当x≤0时，函数的值域为[-1，1]，
当x＞0时，函数的值域为（1，+∞），
故函数f（x）的值域为[-1，+∞），故c正确．
故选：C．
当x＞0时，f（x）=x2+1，为二次函数的一部分，
故f（x）不是单调函数，不是周期函数，也不具备奇偶性，
故可排除A、B、D，
对于C，当x≤0时，函数的值域为[-1，1]，
当x＞0时，函数的值域为（1，+∞），
故函数f（x）的值域为[-1，+∞），故c正确．
故选：C．
点评：本题考查分段函数的应用，考查函数的奇偶性、单调性和周期性，涉及三角函数的性质，属中档题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
某程序框图如右图所示，则输出的n值是（ ）
| A、.21 | B、22 |
| C、．23 | D、．24 |
设集合A={-1，0，1，2}，B={-1，2，3}，则A∩B=（ ）
| A、{-1，0，1，2，3} |
| B、{-1，2} |
| C、{0，1，3} |
| D、{x|-1≤x≤2} |
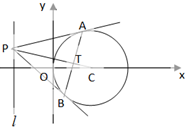已知圆C：（x-2）2+y2=4，从直线l：x=-2上一动点P引圆C的两条切线，切点分别为A，B，PC交AB于T．