题目内容
已知幂函数f(x)=xp2-2p-3(P为整数)的图象关于原点对称,且在(0,+∞)上函数单调递减,解不等式f(x-3)<f(1+2x).
考点:函数单调性的性质
专题:函数的性质及应用,不等式的解法及应用
分析:根据f(x)的图象关于原点对称及在(0,+∞)上单调递减,可求出f(x)=x-3,这时候讨论x-3,1+2x的分布情况,即在(-∞,0),或(0,+∞)上,根据f(x)的单调性及f(x)的符号从而解出原不等式.
解答:
解:∵f(x)在(0,+∞)上单调递减,∴p2-2p-3<0;
解得-1<p<3,若p=0,f(x)=x-3,符合f(x)图象关于原点对称;
若p=1,f(x)=x-4,不符合f(x)图象关于原点对称;
若p=2,f(x)=x-3,符合f(x)图象关于原点对称;
综上得:f(x)=x-3,并且得到f(x)在(-∞,0)单调递减;
①若
,即x<-
,根据f(x)在(-∞,0)单调递减,由原不等式得,x-3>1+2x,解得x<-4;
②若
,即-
<x<3,f(x-3)<0,f(1+2x)>0,满足不等式f(x-3)<f(1+2x);
③若
,即x>3,根据f(x)在(0,+∞)上单调递减,则由原不等式得x-3>1+2x,解得x<-4,不满足x>3,所以这种情况不存在;
综上得原不等式的解集为:(-∞,-4)∪(-
,3).
解得-1<p<3,若p=0,f(x)=x-3,符合f(x)图象关于原点对称;
若p=1,f(x)=x-4,不符合f(x)图象关于原点对称;
若p=2,f(x)=x-3,符合f(x)图象关于原点对称;
综上得:f(x)=x-3,并且得到f(x)在(-∞,0)单调递减;
①若
|
| 1 |
| 2 |
②若
|
| 1 |
| 2 |
③若
|
综上得原不等式的解集为:(-∞,-4)∪(-
| 1 |
| 2 |
点评:考查幂函数的单调性,奇函数的图象关于原点对称,偶函数的图象关于y轴对称,以及根据单调性的定义解不等式.

练习册系列答案
相关题目
已知f(x)=
,则f(3)为( )
|
| A、2 | B、3 | C、4 | D、5 |
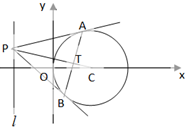 已知圆C:(x-2)2+y2=4,从直线l:x=-2上一动点P引圆C的两条切线,切点分别为A,B,PC交AB于T.
已知圆C:(x-2)2+y2=4,从直线l:x=-2上一动点P引圆C的两条切线,切点分别为A,B,PC交AB于T.