题目内容
已知函数f(x)=
sin(ωx+φ)-cos(ωx+φ)=2sin(ωx+φ-
)为奇函数,且相邻两对称轴间的距离为
.
(1)当x∈(-
,
)时,求f(x)的单调递减区间;
(2)将函数y=f(x)的图象沿x轴方向向右平移
个单位长度,再把横坐标缩短到原来的
(纵坐标不变),得到函数y=g(x)的图象.当x∈[-
,
]时,求函数g(x)的值域.
| 3 |
| π |
| 6 |
| π |
| 2 |
(1)当x∈(-
| π |
| 2 |
| π |
| 4 |
(2)将函数y=f(x)的图象沿x轴方向向右平移
| π |
| 6 |
| 1 |
| 2 |
| π |
| 12 |
| π |
| 6 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)化简函数的解析式为f(x)=2sin(ωx+φ-
),由周期求得ω=2.再根据f(x)为奇函数,求得φ=
,可得f(x)=2sin2x,结合正弦函数的单调性求得f(x)在区间(-
,
)上的减区间.
(2)根据函数y=Asin(ωx+φ)的图象变换规律,求得g(x)=2sin(4x-
),再根据x∈[-
,
]时,利用正弦函数的定义域和值域求得g(x)的值域.
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 4 |
(2)根据函数y=Asin(ωx+φ)的图象变换规律,求得g(x)=2sin(4x-
| π |
| 3 |
| π |
| 12 |
| π |
| 6 |
解答:
解:(1)∵函数f(x)=
sin(ωx+φ)-cos(ωx+φ)=2sin(ωx+φ-
)=2sin(ωx+φ-
),
且相邻两对称轴间的距离为
,可得 T=2×
=
,求得ω=2.
再根据f(x)为奇函数,可得φ-
=kπ,k∈z,即φ=kπ+
,故可取φ=
,故f(x)=2sin2x.
令2kπ+
≤2x≤2kπ+
,求得kπ+
≤x≤kπ+
,可得f(x)的减区间为[kπ+
,kπ+
],k∈z.
再结合x∈(-
,
),可得减区间为[-
,-
].
(2)将函数y=f(x)的图象沿x轴方向向右平移
个单位长度,可得函数y=2sin2(x-
)=2sin(2x-
)的图象;
再把横坐标缩短到原来的
(纵坐标不变),得到函数y=g(x)=2sin(4x-
)的图象,
当x∈[-
,
]时,4x-
∈[-
,
],-1≤sin(2x-
)≤
,∴g(x)∈[-2,
].
| 3 |
| π |
| 6 |
| π |
| 6 |
且相邻两对称轴间的距离为
| π |
| 2 |
| π |
| 2 |
| 2π |
| ω |
再根据f(x)为奇函数,可得φ-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
令2kπ+
| π |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
再结合x∈(-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
(2)将函数y=f(x)的图象沿x轴方向向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
再把横坐标缩短到原来的
| 1 |
| 2 |
| π |
| 3 |
当x∈[-
| π |
| 12 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| 3 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性、定义域和值域,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设集合A={-1,0,1,2},B={-1,2,3},则A∩B=( )
| A、{-1,0,1,2,3} |
| B、{-1,2} |
| C、{0,1,3} |
| D、{x|-1≤x≤2} |
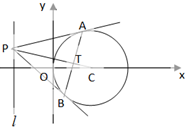 已知圆C:(x-2)2+y2=4,从直线l:x=-2上一动点P引圆C的两条切线,切点分别为A,B,PC交AB于T.
已知圆C:(x-2)2+y2=4,从直线l:x=-2上一动点P引圆C的两条切线,切点分别为A,B,PC交AB于T.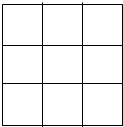 将大小形状相同的4个红球和2个白球放入如图所示的九宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),则所有不同的放法种数为( )
将大小形状相同的4个红球和2个白球放入如图所示的九宫格中,每格至多放一个,要求相邻方格的小球不同色(有公共边的两个方格为相邻),则所有不同的放法种数为( )