题目内容
已知函数f（x）=
，记集合A={（x，y）|y=f（x），x∈R}，实数集为R，映射g：R→A的对应法则是x→（x，f（x）），若这个映射是一一映射，则实数a的取值范围是 ．
|
考点：分段函数的应用
专题：计算题,函数的性质及应用
分析：由x≥1时，f（x）=2x-1+a，是增函数，又映射g是一一映射，则函数f（x）在R上是增函数，则有a＞0，且21-1+a≥a+a，解出即可．
解答：
解：由于f（x）=
，
则x≥1时，f（x）=2x-1+a，是增函数，
又映射g是一一映射，
则函数f（x）在R上是增函数，
则有a＞0，且21-1+a≥a+a，解得0＜a≤1．
故答案为：（0，1]．
|
则x≥1时，f（x）=2x-1+a，是增函数，
又映射g是一一映射，
则函数f（x）在R上是增函数，
则有a＞0，且21-1+a≥a+a，解得0＜a≤1．
故答案为：（0，1]．
点评：本题考查分段函数的应用，考查函数的单调性及运用，注意分界点，属于中档题和易错题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设集合A={-1，0，1，2}，B={-1，2，3}，则A∩B=（ ）
| A、{-1，0，1，2，3} |
| B、{-1，2} |
| C、{0，1，3} |
| D、{x|-1≤x≤2} |
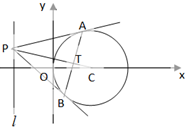已知圆C：（x-2）2+y2=4，从直线l：x=-2上一动点P引圆C的两条切线，切点分别为A，B，PC交AB于T．
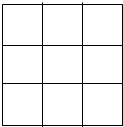将大小形状相同的4个红球和2个白球放入如图所示的九宫格中，每格至多放一个，要求相邻方格的小球不同色（有公共边的两个方格为相邻），则所有不同的放法种数为（ ）