若在甲袋内装有8个白球.4个红球.在乙袋内装有6个白球.6个红球.今从两袋里面各任意取出1个球.设取去的白球的个数为ξ.则下列概率中等于C18C16+C14C16C112C112的是( ) A.PB.PC.PD.P 题目和参考答案——青夏教育精英家教网——

题目内容

若在甲袋内装有8个白球，4个红球，在乙袋内装有6个白球，6个红球，今从两袋里面各任意取出1个球，设取去的白球的个数为ξ，则下列概率中等于

C

1

8

C

1

6

+

C

1

4

C

1

6

C

1

12

C

1

12

的是（　　）

A、P（ξ=0）

B、P（ξ≤2）

C、P（ξ=1）

D、P（ξ=2）

考点：离散型随机变量的期望与方差

专题：概率与统计

分析：由已知条件，分别求出P（ξ=0），P（ξ≤2），P（ξ=1），P（ξ=2）的值，由此能求出答案．

解答： 解：由题意知P（ξ=0）=

C

1

4

C

1

6

C

1

12

C

1

12

，
P（ξ≤2）=1-

C

1

8

C

1

6

+

C

1

4

C

1

6

C

1

12

C

1

12

，
P（ξ=1）=

C

1

8

C

1

6

+

C

1

4

C

1

6

C

1

12

C

1

12

，
P（ξ=2）=

C

1

8

C

1

6

C

1

12

C

1

12

，
故选：C．

点评：本题考查概率的求法，考查离散型随机变量的分布列、数学期望的求法，是中档题，解题时要认真审题．

练习册系列答案

暑假作业北京艺术与科学电子出版社系列答案

黄冈状元成才路暑假作业新疆人民出版社系列答案

暑假特训浙江大学出版社系列答案

名师一号假期作业暑假作业河北教育出版社系列答案

第三学期赢在暑假系列答案

暑假作业宁夏人民教育出版社系列答案

优化学习暑假40天江苏人民出版社系列答案

快乐暑假学段衔接提升方案新疆美术摄影出版社系列答案

假期作业济南出版社系列答案

快乐假期暑假生活延边人民出版社系列答案

相关题目

tan(π+α)cos(2π+α)sin(α-

cos(-α-3π)sin(-3π-α)

画出函数y=x|2-x|的图象，根据图象写出这个函数的定义域和值域．

根据函数单调性定义，判断并证明函数y=

，a≠1在区间（-1，1）上的单调性．

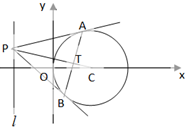已知圆C：（x-2）²+y²=4，从直线l：x=-2上一动点P引圆C的两条切线，切点分别为A，B，PC交AB于T．
（1）求点T的轨迹方程；
（2）求S_△ABC的最大值．

如图，已知在四棱锥P-ABCD中，AB∥CD，E、F、G分别是PC、PD、BC中点，证明：平面PAB∥平面EFG．

已知△ABC中，已知cosA=-

sinB．
（1）求sinC的值．
（2）若a=

，求△ABC的面积．

已知在△ABC中，两中线AD、BE互相垂直，求

对任意实数x，（a²-1）x²+（a-1）x-1＜0都成立，则a的取值范围是