题目内容
 某厂生产一种内径为105mm的零件,为了检查该生产流水线的质量情况,随机抽取该流水线上50个零件作为样本测出它们的内径长度(单位:mm),长度的分组区间为[90,95),[95,100),[100,105),[105,110),[110,115),由此得到样本的频率分布直方图,如图所示.已知内径长度在[100,110)之间的零件被认定为一等品,在[95,100)或[110,115)之间的零件被认定为二等品,否则认定为次品.
某厂生产一种内径为105mm的零件,为了检查该生产流水线的质量情况,随机抽取该流水线上50个零件作为样本测出它们的内径长度(单位:mm),长度的分组区间为[90,95),[95,100),[100,105),[105,110),[110,115),由此得到样本的频率分布直方图,如图所示.已知内径长度在[100,110)之间的零件被认定为一等品,在[95,100)或[110,115)之间的零件被认定为二等品,否则认定为次品.(1)从上述样品中随机抽取1个零件,求恰好是一个次品的概率;
(2)以上述样本数据来估计该流水线的总体数据,若从流水线上(产品众多)任意抽取3个零件,设一等品的数量为X,求X的分布列及数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(1)根据频率分布直方图的矩形面积等于该组的概率,累加长度在[9,115)之间的频率,进而根据累积频率为1,可得答案;
(2)由频率分布直方图中各组的频率,分别算出P(X=0),P(X=1),P(X=2),P(X=3)的值,即可得到随机变量X的分布列,然后代入数学期望公式,可进而求出数学期望.
(2)由频率分布直方图中各组的频率,分别算出P(X=0),P(X=1),P(X=2),P(X=3)的值,即可得到随机变量X的分布列,然后代入数学期望公式,可进而求出数学期望.
解答:
解:(1)在[100,110)上的矩形面积为(0.032+0.08+0.06+0.02)×5=0.96,
1-0.96=0.04
∴估计从该流水线上任取一件产品,恰好为一个次品的概率为0.04;
(2)由题意知,X的取值为0,1,2,3,
∵上述样品中随机抽取1个零件,恰为一等品的概率为:(0.08+0.06)×5=0.7,
P(X=0)=C30×0.33=0.027,
P(X=1)=C31×0.7×0.32=0.189,
P(X=2)=C32×0.72×0.3=0.441,
P(X=3)=C33×0.73=0.343.
故随机变量X的分布列为
∴E(X)=1×0.189+2×0.441+3×0.343=2.09
1-0.96=0.04
∴估计从该流水线上任取一件产品,恰好为一个次品的概率为0.04;
(2)由题意知,X的取值为0,1,2,3,
∵上述样品中随机抽取1个零件,恰为一等品的概率为:(0.08+0.06)×5=0.7,
P(X=0)=C30×0.33=0.027,
P(X=1)=C31×0.7×0.32=0.189,
P(X=2)=C32×0.72×0.3=0.441,
P(X=3)=C33×0.73=0.343.
故随机变量X的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | 0.027 | 0.189 | 0.441 | 0.343 |
点评:本题主要考查了离散型随机变量的期望和分布列,以及频率分布直方图,同时考查了识图能力,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
在平面直角坐标系xOy上的区域D由不等式|x+2|+|y+2|≤2给定.则区域D的面积等于( )
| A、2 | ||
| B、4 | ||
C、4
| ||
| D、8 |
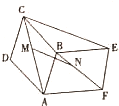 如图所示,ABCD-ABEF都是平行四边形,且不共面,M、N分别是AC、BF的中点,判断
如图所示,ABCD-ABEF都是平行四边形,且不共面,M、N分别是AC、BF的中点,判断