题目内容
若向量
=（
，cos2x+
），
=（sin2x，2）．
（1）当x∈[0，
]时
•
的最大值为6，求m的值；
（2）设f（x）=
•
，当x∈R时，求f（x）的最小值及对应的x的取值集合．
| a |
| 3 |
| m |
| 2 |
| b |
（1）当x∈[0，
| π |
| 2 |
| a |
| b |
（2）设f（x）=
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,三角函数的求值,平面向量及应用
分析：（1）运用向量的数量积的坐标公式和二倍角的余弦公式以及两角和的正弦公式，再由正弦函数的最值性质，即可求得m；
（2）由（1）得到f（x）的函数式，再由正弦函数的最值性，即可得到最小值和相应x的集合．
（2）由（1）得到f（x）的函数式，再由正弦函数的最值性，即可得到最小值和相应x的集合．
解答：
解：（1）向量
=（
，cos2x+
），
=（sin2x，2），
则
•
=
sin2x+2cos2x+m
=
sin2x+cos2x+1+m=2sin(2x+
)+1+m，
由于0≤x≤
，即0≤x≤π，则
≤2x+
≤
，
则有当2x+
=
即x=
时，则有sin(2x+
)最大值为1．
故由
•
的最大值为6，即6=2+1+m，解得m=3；
（2）由（1）得，f(x)=2sin(2x+
)+4，
当x∈R，f（x）的最小值为-2，
此时2x+
=2kπ-
即x的取值集合为{x|x=kπ-
(k∈Z)}．
| a |
| 3 |
| m |
| 2 |
| b |
则
| a |
| b |
| 3 |
=
| 3 |
| π |
| 6 |
由于0≤x≤
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
则有当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
故由
| a |
| b |
（2）由（1）得，f(x)=2sin(2x+
| π |
| 6 |
当x∈R，f（x）的最小值为-2，
此时2x+
| π |
| 6 |
| π |
| 2 |
即x的取值集合为{x|x=kπ-
| π |
| 3 |
点评：本题考查平面向量的数量积及运用，考查三角恒等变换公式的运用，考查正弦函数的性质和运用，考查运算能力，属于中档题．
练习册系列答案
相关题目
某厂生产一种内径为105mm的零件，为了检查该生产流水线的质量情况，随机抽取该流水线上50个零件作为样本测出它们的内径长度（单位：mm），长度的分组区间为[90，95），[95，100），[100，105），[105，110），[110，115），由此得到样本的频率分布直方图，如图所示．已知内径长度在[100，110）之间的零件被认定为一等品，在[95，100）或[110，115）之间的零件被认定为二等品，否则认定为次品．
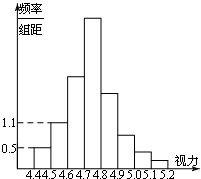为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图，由于不慎将部分数据丢失，但知道后5组的频数成等比数列，设视力在4.6到4.9之间的学生数为a，最大频率为b，则a，b的值分别为（ ）| A、77，0.53 |
| B、70，0.32 |
| C、77，5.3 |
| D、70，3.2 |
下列有关命题的说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1” |
| B、“x=-1”是“x2-2x-3=0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x-1＜0”的否定是“?x∈R，均有x2+x-1＞0” |
| D、命题“已知x，y∈R，若x+y≠5，则x≠1或y≠4”为真命题 |