题目内容
已知函数f（x）=ax+
-2a+2（a＞0）的图象在点（1，f（1））处的切线与直线y=2x+1平行．
（Ⅰ）求log4（a-b）的值；
（Ⅱ）若f（x）-2lnx≥0在[1，+∞）上恒成立，求a的取值范围．
| b |
| x |
（Ⅰ）求log4（a-b）的值；
（Ⅱ）若f（x）-2lnx≥0在[1，+∞）上恒成立，求a的取值范围．
考点：导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：（Ⅰ）由已知得f′(x)=a-
，由此能求出log4（a-b）=log42=
．
（Ⅱ）令g（x）=f（x）-2lnx=ax+
+2-2a-2lnx，得g（1）=0，g′（x）=a-
-
=
，由此利用分类讨论思想能求出a的取值范围．
| b |
| x2 |
| 1 |
| 2 |
（Ⅱ）令g（x）=f（x）-2lnx=ax+
| a-2 |
| x |
| a-2 |
| x2 |
| 2 |
| x |
a(x-1)(x-
| ||
| x2 |
解答：
解：（Ⅰ）∵f（x）=ax+
-2a+2（a＞0），
∴f′(x)=a-
，
∵函数f（x）=ax+
-2a+2（a＞0）的图象在点（1，f（1））处的切线与直线y=2x+1平行，
∴f′（1）=a-b=2，
∴log4（a-b）=log42=
．
（Ⅱ）由（Ⅰ）得f（x）=ax+
+2-2a，
令g（x）=f（x）-2lnx=ax+
+2-2a-2lnx，x∈[1，+∞），
则g（1）=0，
g′（x）=a-
-
=
=
，
①当0＜a＜1时，
＞1，
∴当x∈（1，
）时，g′（x）＜0，函数g（x）是（1，
）上的减函数，
∴f（x）-2lnx≥0在[1，+∞）上不成立；
②当a＞1时，则
＜0，
当x＞1时，g′（x）＞0，
解得g（x）在[1，+∞）上单调递增，
又g（1）=0，∴f（x）-2lnx＞0．
综上，a的取值范围是[1，+∞）．
| b |
| x |
∴f′(x)=a-
| b |
| x2 |
∵函数f（x）=ax+
| b |
| x |
∴f′（1）=a-b=2，
∴log4（a-b）=log42=
| 1 |
| 2 |
（Ⅱ）由（Ⅰ）得f（x）=ax+
| a-2 |
| x |
令g（x）=f（x）-2lnx=ax+
| a-2 |
| x |
则g（1）=0，
g′（x）=a-
| a-2 |
| x2 |
| 2 |
| x |
=
| ax2-2x-(a-2) |
| x2 |
=
a(x-1)(x-
| ||
| x2 |
①当0＜a＜1时，
| 2-a |
| a |
∴当x∈（1，
| 2-a |
| a |
| 2-a |
| a |
∴f（x）-2lnx≥0在[1，+∞）上不成立；
②当a＞1时，则
| 2-a |
| a |
当x＞1时，g′（x）＞0，
解得g（x）在[1，+∞）上单调递增，
又g（1）=0，∴f（x）-2lnx＞0．
综上，a的取值范围是[1，+∞）．
点评：本题考查对数值的求法，考查实数的取值范围的求法，是中档题，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
相关题目
某厂生产一种内径为105mm的零件，为了检查该生产流水线的质量情况，随机抽取该流水线上50个零件作为样本测出它们的内径长度（单位：mm），长度的分组区间为[90，95），[95，100），[100，105），[105，110），[110，115），由此得到样本的频率分布直方图，如图所示．已知内径长度在[100，110）之间的零件被认定为一等品，在[95，100）或[110，115）之间的零件被认定为二等品，否则认定为次品．
如图是调查某地某公司1000名员工的月收入后制作的直方图．根据直方图估计：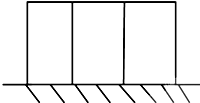
用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍，且鸡舍内用相同的篱笆隔成三间（如图所示），如果挨着墙的边长为x，鸡舍面积为y