题目内容
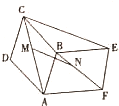如图所示，ABCD-ABEF都是平行四边形，且不共面，M、N分别是AC、BF的中点，判断| CE |
| MN |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：因为ABCD-ABEF都是平行四边形，所以连接AE，交于N，M，N分别是AC，AE的中点，所以MN∥CE．
解答：
解：∵ABCD-ABEF都是平行四边形，
∵M，N分别是AC，AE的中点，连接AE，交于N，
∴MN是△ACE的中位线
∴MN∥CE，
∴
∥
．
∵M，N分别是AC，AE的中点，连接AE，交于N，
∴MN是△ACE的中位线
∴MN∥CE，
∴
| CE |
| MN |
点评：本题考查了空间线线关系的判断；属于基础题．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
若直线y=kx+1与椭圆
+
=1恒有公共点，则m的取值范围是（ ）
| x2 |
| 2014 |
| y2 |
| m |
| A、[1，2014）∪（2014，+∞） |
| B、[1，2014） |
| C、[1，+∞） |
| D、（2014，+∞） |
某厂生产一种内径为105mm的零件，为了检查该生产流水线的质量情况，随机抽取该流水线上50个零件作为样本测出它们的内径长度（单位：mm），长度的分组区间为[90，95），[95，100），[100，105），[105，110），[110，115），由此得到样本的频率分布直方图，如图所示．已知内径长度在[100，110）之间的零件被认定为一等品，在[95，100）或[110，115）之间的零件被认定为二等品，否则认定为次品．不等式ax2-x-c＞0的解集为{x|-2＜x＜1}，则函数y=ax2+x-c的零点为（ ）
| A、（-1，0）和（2，0） |
| B、（-1，0） |
| C、（2，0） |
| D、-1和2 |