题目内容
函数y=2x2-2x，x∈（0，3）的值域为 ．
考点：复合函数的单调性
专题：计算题,函数的性质及应用
分析：令t=x2-2x，x∈（0，3），对称轴x=1∈（0，3），x=1时，t取最小值-1，x=0时，y=0；x=3时，y=3．则-1≤t＜3．则y=2t，由增函数的性质即可得到值域．
解答：
解：令t=x2-2x，x∈（0，3），对称轴x=1∈（0，3），
x=1时，t取最小值-1，x=0时，y=0；x=3时，y=3．
则-1≤t＜3．
则y=2t，为增函数，故有
≤y＜8，
即值域为[
，8）．
故答案为：[
，8）．
x=1时，t取最小值-1，x=0时，y=0；x=3时，y=3．
则-1≤t＜3．
则y=2t，为增函数，故有
| 1 |
| 2 |
即值域为[
| 1 |
| 2 |
故答案为：[
| 1 |
| 2 |
点评：本题考查复合函数的单调性，考查指数函数的单调性和二次函数的单调性及运用，考查运算能力，属于中档题．
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
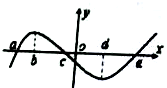
已知定义在R的函数f（x），其导函数f′（x）的部分图象如图所示，则下列判断一定正确的是（ ）
| A、f（a）=f（c）=f（e） |
| B、f（b）＞f（c）＞f（d） |
| C、f（c）＞f（b）＞f（a） |
| D、f（c）＞f（d）＞f（a） |
某厂生产一种内径为105mm的零件，为了检查该生产流水线的质量情况，随机抽取该流水线上50个零件作为样本测出它们的内径长度（单位：mm），长度的分组区间为[90，95），[95，100），[100，105），[105，110），[110，115），由此得到样本的频率分布直方图，如图所示．已知内径长度在[100，110）之间的零件被认定为一等品，在[95，100）或[110，115）之间的零件被认定为二等品，否则认定为次品．