题目内容
根据市场调查结果,预测某种家用商品从年初开始的n个月内累积的需求量Sn(万件)近似地满足关系式Sn=
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是 .
| n |
| 90 |
考点:数列的求和
专题:等差数列与等比数列
分析:利用“当n=1时,a1=S1.n≥2时,an=Sn-Sn-1”求出an,解出an>1.5即可得出.
解答:
解:当n=1时,a1=S1=
.
n≥2时,an=Sn-Sn-1=
(21n-n2-5)-
[21(n-1)-(n-1)2-5]
=
>1.5,
化为n2-15n+54<0,
解得6<n<9.
可知当n=7或8,需求量超过1.5万件.
故答案为:7,8.
| 1 |
| 6 |
n≥2时,an=Sn-Sn-1=
| n |
| 90 |
| n-1 |
| 90 |
=
| -3n2+45n-27 |
| 90 |
化为n2-15n+54<0,
解得6<n<9.
可知当n=7或8,需求量超过1.5万件.
故答案为:7,8.
点评:本题考查了利用“当n=1时,a1=S1.n≥2时,an=Sn-Sn-1”求出an,考查了一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
过点(-l,3)且与直线x-2y+3=0垂直的直线方程是( )
| A、x-2y+7=0 |
| B、2x-y+5=0 |
| C、2x+y-5=0 |
| D、2x+y-1=0 |
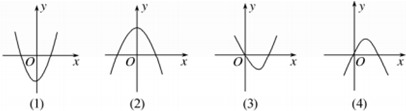
下图,有一个是函数f(x)=
x3+ax2+(a2-1)x+1(a∈R,a≠0)
x3+ax2+(a2-1)2+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)等于( )
| 1 |
| 3 |
| 1 |
| 3 |

A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设直线l1、l2的方向向量分别为
=(0,-3,3),
=(-1,1,0),则直线l1、l2的夹角是( )
| a |
| b |
| A、30° | B、45° |
| C、60° | D、120° |