题目内容
下图,有一个是函数f(x)=
x3+ax2+(a2-1)x+1(a∈R,a≠0)
x3+ax2+(a2-1)2+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)等于( )
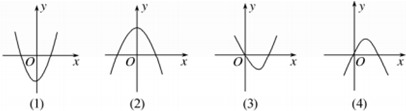
| 1 |
| 3 |
| 1 |
| 3 |

A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:函数的图象,导数的运算
专题:函数的性质及应用
分析:求出导函数,据导函数的二次项系数为正得到图象开口向上;利用函数解析式中有2ax,故函数不是偶函数,得到函数的图象.
解答:
解:∵f′(x)=x2+2ax+(a2-1),
∴导函数f′(x)的图象开口向上.
又∵a≠0,
∴f(x)不是偶函数,其图象不关于y轴对称
其图象必为第三张图.由图象特征知f′(0)=0,
且对称轴-a>0,
∴a=-1.
∴f(x)=
x3-x2+1
∴f(-1)=-
-1+1=-
,
故选:B
∴导函数f′(x)的图象开口向上.
又∵a≠0,
∴f(x)不是偶函数,其图象不关于y轴对称
其图象必为第三张图.由图象特征知f′(0)=0,
且对称轴-a>0,
∴a=-1.
∴f(x)=
| 1 |
| 3 |
∴f(-1)=-
| 1 |
| 3 |
| 1 |
| 3 |
故选:B
点评:本题考查导函数的运算法则、二次函数的图象与二次函数系数的关系:开口方向与二次项系数的符号有关、对称轴公式.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
复数z=log2(m2-3m-3)+ilog2(3-m)(m∈R),如果a是纯虚数,则m的值为( )
| A、-1或4 | B、-1 | C、4 | D、3 |
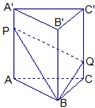 如图直三棱柱ABC-A1B1C1的体积为120,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为
如图直三棱柱ABC-A1B1C1的体积为120,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为