题目内容
函数y=ex-elnx的最小值为 .
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用,导数的综合应用
分析:由题意,y=ex-elnx的定义域为(0,+∞),求导从而确定y=ex-elnx在(0,1)上单调递减,在(1,+∞)上单调递增,从而求最小值.
解答:
解:y=ex-elnx的定义域为(0,+∞),
y′=ex-
=
,
故当x>1时,y′>0,
当0<x<1时,y′<0,
故y=ex-elnx在(0,1)上单调递减,在(1,+∞)上单调递增,
故当x=1时,y=ex-elnx取得最小值,
即最小值为e-e=0.
故答案为:0.
y′=ex-
| e |
| x |
| xex-e |
| x |
故当x>1时,y′>0,
当0<x<1时,y′<0,
故y=ex-elnx在(0,1)上单调递减,在(1,+∞)上单调递增,
故当x=1时,y=ex-elnx取得最小值,
即最小值为e-e=0.
故答案为:0.
点评:本题考查了函数的最值的求法,同时考查了导数的综合应用,属于中档题

练习册系列答案
相关题目
下列命题的说法错误的是( )
| A、若p∧q为假命题,则p,q均为假命题. |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件. |
| C、对于命题p:?x∈R,x2+x+1>0,则?p:?x∈R,x2+x+1≤0. |
| D、命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
下列命题中,真命题是( )
| A、?x0∈R,e x0≤0 | ||||||||||||||||
| B、?x∈R,2x>x2 | ||||||||||||||||
| C、“a>1,b>1”是“ab>1”的充要条件 | ||||||||||||||||
D、设
|
6个同学任意选3个参加一个会议,共有选法种数( )种.
| A、15 | B、10 | C、60 | D、20 |
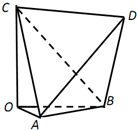 如图,多面体OABCD,AB=CD=2,AD=BC=2
如图,多面体OABCD,AB=CD=2,AD=BC=2