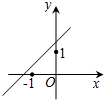题目内容
下列命题的说法错误的是( )
| A、若p∧q为假命题,则p,q均为假命题. |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件. |
| C、对于命题p:?x∈R,x2+x+1>0,则?p:?x∈R,x2+x+1≤0. |
| D、命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A:p∧q为假命题时,p假q真,或p真q假,或p,q均为假命题;
B:判断充分性与必要性是否成立即可;
C:根据全称命题的否定是特称命题进行判断;
D:根据命题与它的逆否命题的关系进行判断即可.
B:判断充分性与必要性是否成立即可;
C:根据全称命题的否定是特称命题进行判断;
D:根据命题与它的逆否命题的关系进行判断即可.
解答:
解:对于A,当p∧q为假命题时,p假q真,或p真q假,或p,q均为假命题,∴A错误;
对于B,x=1时,x2-3x+2=0,充分性成立,
x2-3x+2=0时,x=1或x=2,必要性不成立,∴是充分不必要条件,B正确;
对于C,当命题p:?x∈R,x2+x+1>0时,它的否定是¬p:?x∈R,x2+x+1≤0,∴C正确;
对于D,命题“若x2-3x+2=0,则x=1”的逆否命题是:“若x≠1,则x2-3x+2≠0”,∴D正确.
故选:A.
对于B,x=1时,x2-3x+2=0,充分性成立,
x2-3x+2=0时,x=1或x=2,必要性不成立,∴是充分不必要条件,B正确;
对于C,当命题p:?x∈R,x2+x+1>0时,它的否定是¬p:?x∈R,x2+x+1≤0,∴C正确;
对于D,命题“若x2-3x+2=0,则x=1”的逆否命题是:“若x≠1,则x2-3x+2≠0”,∴D正确.
故选:A.
点评:本题通过命题真假的判断,考查了复合命题的真假性,充分与必要条件,全称命题与特称命题以及四种命题真假的关系的应用问题,是综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设实数x和y满足约束条件
,且z=ax+y取得最小值的最优解仅为点A(1,2),则实数a的取值范围是( )
|
A、(-∞,-
| ||
B、(-∞,-
| ||
C、(
| ||
D、[
|
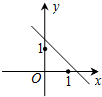
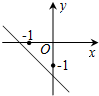
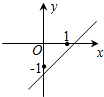
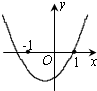 已知二次函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是( )
已知二次函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是( )