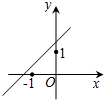题目内容
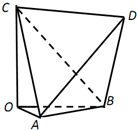 如图,多面体OABCD,AB=CD=2,AD=BC=2
如图,多面体OABCD,AB=CD=2,AD=BC=2| 3 |
| 10 |
①三棱锥O-ABC的体积是定值;
②球面经过点A、B、C、D四点的球的直径是
| 13 |
③直线OB∥平面ACD;
④直线AD与OB所成角是60°;
⑤二面角A-OC-D等于30°.
其中正确的结论是
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:由题意,只要构造长方体,设OA=x,OB=y,OC=z,则x2+y2=4,x2+z2=10,y2+z2=12,解得,x=1,y=
,z=3,运用棱锥的体积公式,即可判断①;运用异面直线所成角的定义,即可判断②;球面经过点A、B、C、D两点的球的直径即为长方体的对角线长,即可判断③;由于OB∥AE,AE和平面ACD相交,即可判断④.
| 3 |
解答:
 解:由题意,构造长方体,如右图,设OA=x,OB=y,OC=z,
解:由题意,构造长方体,如右图,设OA=x,OB=y,OC=z,
则x2+y2=4,x2+z2=10,y2+z2=12,解得,x=1,y=
,z=3,
对于①,三棱锥O-ABC的体积为
OC×
OA×OB=
,故①对;
对于②,球面经过点A、B、C、D两点的球的直径即为长方体的对角线长,
即为
=
,故②对;
对于③,由于OB∥AE,AE和平面ACD相交,则OB和平面ACD相交,故③错.
对于④,由于OB∥AE,则∠DAE即为直线AD与OB所成的角,
由tan∠DAE=
=
,则∠DAE=60°,故④对;
⑤因为AO⊥OC,DC⊥OC,所以异面直线CD与OA所成的角大小为二面角A-OC-D的二面角大小,连接OE,则角AOE为所求,tan∠AOE=
=
,所以∠AOE=60°;⑤错误;
故答案为:①②④
 解:由题意,构造长方体,如右图,设OA=x,OB=y,OC=z,
解:由题意,构造长方体,如右图,设OA=x,OB=y,OC=z,则x2+y2=4,x2+z2=10,y2+z2=12,解得,x=1,y=
| 3 |
对于①,三棱锥O-ABC的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
对于②,球面经过点A、B、C、D两点的球的直径即为长方体的对角线长,
即为
12+32+(
|
| 13 |
对于③,由于OB∥AE,AE和平面ACD相交,则OB和平面ACD相交,故③错.
对于④,由于OB∥AE,则∠DAE即为直线AD与OB所成的角,
由tan∠DAE=
| DE |
| AE |
| 3 |
⑤因为AO⊥OC,DC⊥OC,所以异面直线CD与OA所成的角大小为二面角A-OC-D的二面角大小,连接OE,则角AOE为所求,tan∠AOE=
| AE |
| OA |
| 3 |
故答案为:①②④
点评:本题考查线面的位置关系的判断,空间异面直线所成的角,以及三棱锥的体积的计算和多面体的外接球的关系,考查运算能力,属于中档题和易错题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设a=50.8,b=0.67,c=log0.74,则a,b,c的大小关系是( )
| A、a<c<b |
| B、c<a<b |
| C、b<a<c |
| D、c<b<a |
设实数x和y满足约束条件
,且z=ax+y取得最小值的最优解仅为点A(1,2),则实数a的取值范围是( )
|
A、(-∞,-
| ||
B、(-∞,-
| ||
C、(
| ||
D、[
|
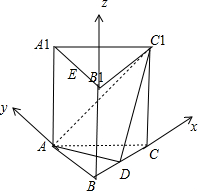 (理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.
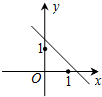
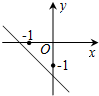
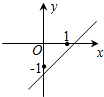
(理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.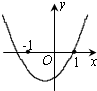 已知二次函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是( )
已知二次函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是( )