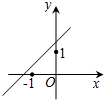题目内容
下列命题中，真命题是（ ）
| A、?x0∈R，e x0≤0 | ||||||||||||||||
| B、?x∈R，2x＞x2 | ||||||||||||||||
| C、“a＞1，b＞1”是“ab＞1”的充要条件 | ||||||||||||||||
D、设
|
考点：命题的真假判断与应用
专题：简易逻辑
分析：利用特称命题的真假判断A的正误；全称命题的真假判断B的正误；充要条件判断C的正误；向量与怎样添加的关系判断D的正误．
解答：
解：对于A，?x0∈R，e x0＞0，所以A不正确；
对于B，?x∈R，2x＞x2，当x=2时，不等式不成立，所以B不正确；
对于C，“a＞1，b＞1”是“ab＞1”的充分不必要条件，所以C不正确；
对于D，设
，
为向量，则“|
•
|=|
||
|”说明两个向量的夹角为0°或180°，所以“|
•
|=|
||
|”是“
∥
”的充要条件，所以D正确．
故选：D．
对于B，?x∈R，2x＞x2，当x=2时，不等式不成立，所以B不正确；
对于C，“a＞1，b＞1”是“ab＞1”的充分不必要条件，所以C不正确；
对于D，设
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故选：D．
点评：本题考查命题的真假的判断与应用，特称命题与全称命题的关系，充要条件的判断，基本知识的考查．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
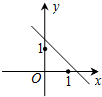
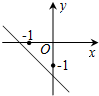
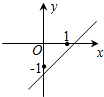
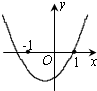已知二次函数f（x）=（x-a）（x-b）（其中a＞b）的图象如图所示，则函数g（x）=ax+b的图象是（ ）
