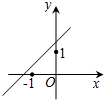题目内容
已知集合A={x|x2-x-12<0},集合B={x|x2+2x-8>0},集合C={x|x2-4ax+3a2<0}.
(1)求A∩(CRB);
(2)若C?(A∩B),试确定实数a的取值范围.
(1)求A∩(CRB);
(2)若C?(A∩B),试确定实数a的取值范围.
考点:其他不等式的解法,交、并、补集的混合运算
专题:不等式的解法及应用,集合
分析:(1)通过二次不等式的解法求出集合A、B,然后求出集合B的补集,即可求解A∩(CRB);
(2)求出A、B的交集,判断集合的关系,转化为不等式组求解a的范围即可.
(2)求出A、B的交集,判断集合的关系,转化为不等式组求解a的范围即可.
解答:
解:(1)依题意得:集合A={x|x2-x-12<0}={x|-3<x<4},集合B={x|x2+2x-8>0}={x|x<-4或x>2},CRB={x|-4≤x≤2},A∩(CRB)={x|-3<x≤2};…(6分)
(2)∴A∩B={x|2<x<4},∵C?(A∩B),∴{x|2<x<4}是,x2-4ax+3a2<0解集的子集,
可得:
,
即:
,
解得:
,
解得a∈[
,2].
(2)∴A∩B={x|2<x<4},∵C?(A∩B),∴{x|2<x<4}是,x2-4ax+3a2<0解集的子集,
可得:
|
即:
|
解得:
|
解得a∈[
| 4 |
| 3 |
点评:本题考查不等式组以及二次不等式的解法,集合的交并补的运算,考查计算能力以及转化思想.

练习册系列答案
相关题目
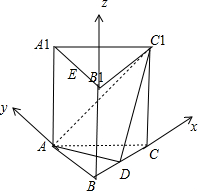 (理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.
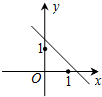
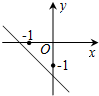
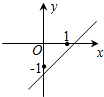
(理)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1=2,∠ABC=90°,D是BC的中点.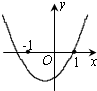 已知二次函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是( )
已知二次函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是( )