题目内容
若△ABC中,已知
•
=tanA,当A=
时,△ABC的面积为 .
| AB |
| AC |
| π |
| 6 |
考点:平面向量数量积的运算,三角形的面积公式
专题:平面向量及应用
分析:由条件利用两个向量的数量积的定义,求得AB•AC=
,再根据△ABC的面积为
AB•AC•sinA,计算求得结果.
| 2 |
| 3 |
| 1 |
| 2 |
解答:
解:△ABC中,∵
•
=AB•AC•cosA=tanA,
∴当A=
时,有 AB•AC•
=
,解得AB•AC=
,
△ABC的面积为
AB•AC•sinA=
×
×
=
,
故答案为:
.
| AB |
| AC |
∴当A=
| π |
| 6 |
| ||
| 2 |
| ||
| 3 |
| 2 |
| 3 |
△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题主要考查两个向量的数量积的定义,三角形的面积公式,属于基础题.

练习册系列答案
相关题目

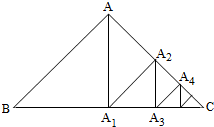 如图,在等腰直角三角形ABC中,斜边BC=2
如图,在等腰直角三角形ABC中,斜边BC=2