题目内容
已知x,y满足约束条件
,当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2
时,a2+b2的最小值为( )
|
| 5 |
| A、5 | ||
| B、4 | ||
C、
| ||
| D、2 |
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件正常可行域,然后求出使目标函数取得最小值的点的坐标,代入目标函数得到2a+b-2
=0.a2+b2的几何意义为坐标原点到直线2a+b-2
=0的距离的平方,然后由点到直线的距离公式得答案.
| 5 |
| 5 |
解答:
解:由约束条件
作可行域如图,
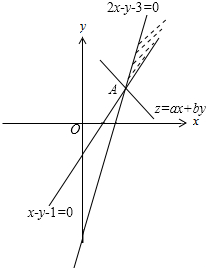
联立
,解得:A(2,1).
化目标函数为直线方程得:y=-
x+
(b>0).
由图可知,当直线y=-
x+
过A点时,直线在y轴上的截距最小,z最小.
∴2a+b=2
.
即2a+b-2
=0.
则a2+b2的最小值为(
)2=4.
故选:B.
|

联立
|
化目标函数为直线方程得:y=-
| a |
| b |
| z |
| b |
由图可知,当直线y=-
| a |
| b |
| z |
| b |
∴2a+b=2
| 5 |
即2a+b-2
| 5 |
则a2+b2的最小值为(
-2
| ||
|
故选:B.
点评:本题考查简单的线性规划,考查数形结合的解题思想方法,考查了数学转化思想方法,训练了点到直线距离公式的应用,是中档题.

练习册系列答案
相关题目
若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为( )
| A、5或8 | B、-1或5 |
| C、-1或-4 | D、-4或8 |
阅读如图的程序框图,则输出的S为( )


| A、6 | B、10 | C、14 | D、30 |
已知a,b∈R,i是虚数单位,若a-i与2+bi互为共轭复数,则(a+bi)2=( )
| A、5-4i | B、5+4i |
| C、3-4i | D、3+4i |
若α,β为两个不同的平面,m、n为不同直线,下列推理:
①若α⊥β,m⊥α,n⊥β,则直线m⊥n;
②若直线m∥平面α,直线n⊥直线m,则直线n⊥平面α;
③若直线m∥n,m⊥α,n?β,则平面α⊥平面β;
④若平面α∥平面β,直线m⊥平面β,n?α,则直线m⊥直线n;
其中正确说法的序号是( )
①若α⊥β,m⊥α,n⊥β,则直线m⊥n;
②若直线m∥平面α,直线n⊥直线m,则直线n⊥平面α;
③若直线m∥n,m⊥α,n?β,则平面α⊥平面β;
④若平面α∥平面β,直线m⊥平面β,n?α,则直线m⊥直线n;
其中正确说法的序号是( )
| A、③④ | B、①③④ |
| C、①②③④ | D、①④ |
在x(1+x)6的展开式中,含x3项的系数为( )
| A、30 | B、20 | C、15 | D、10 |