Question

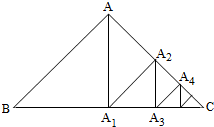如图，在等腰直角三角形ABC中，斜边BC=2

2

，过点A作BC的垂线，垂足为A₁，过点A₁作AC的垂线，垂足为A₂，过点A₂作A₁C的垂线，垂足为A₃…，依此类推，设BA=a₁，AA₁=a₂，A₁A₂=a₃，…，A₅A₆=a₇，则a₇=

 

．

Answer 1

考点：归纳推理

专题：等差数列与等比数列

分析：根据条件确定数列{a_n}是等比数列，即可得到结论．

解答： 解：∵等腰直角三角形ABC中，斜边BC=2

2

，
∴sin45°=

AA1

AB

=

2

2

，即

a2

a1

=

2

2

，
同理

a3

a2

=

2

2

，

a4

a3

=

2

2

，
由归纳推理可得{a_n}是公比q=

2

2

的等比数列，首项a₁=2，
则a₇=2•(

2

2

)6=

1

4

，
故答案为：

1

4

．

点评：本题主要考查归纳推理的应用，根据等腰直角三角形之间的关系，得到数列{a_n}是公比q=

2

2

的等比数列是解决本题的关键．