题目内容
10.在△ABC中,D在边BC上,且BD=2,DC=1,∠B=30°,∠ADC=150°,AB的长为$\frac{2\sqrt{3}}{3}$;△ABC的面积$\frac{\sqrt{3}}{2}$.分析 由题意,∠ADC=150°,则,∠ADB=30°,∠B=30°,可得AB=AD.利用余弦定理可得AB的长度.根据△ABC的面积S=$\frac{1}{2}$AB•BC•sinB可得答案.
解答 解:由题意D在边BC上,∠ADC=150°,
∴,∠ADB=30°,∠B=30°,
∴AB=AD.
余弦定理可得:cos30°=$\frac{A{B}^{2}+B{D}^{2}-A{D}^{2}}{2AB•BD}$,BD=2,
可得:AB=AD=$\frac{2\sqrt{3}}{3}$
DC=1,则BC=3
△ABC的面积S=$\frac{1}{2}$AB•BC•sinB=$\frac{1}{2}×\frac{2\sqrt{3}}{3}×3×\frac{1}{2}$=$\frac{\sqrt{3}}{2}$
故答案为:$\frac{2\sqrt{3}}{3}$,$\frac{\sqrt{3}}{2}$
点评 本题考查三角形的余弦定理的运用,考查运算能力,属于基础题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
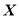 为取出的3个球中编号的最小值,求
为取出的3个球中编号的最小值,求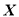 的分布列与数学期望.
的分布列与数学期望.