题目内容
5.已知f(x)=3x2-2xf′(2),则f′(2)=4.分析 根据题意,对f(x)=3x2-2xf′(2)求导可得f′(x)=6x-2f′(2),令x=2,分析可得f′(2)=12-2f′(2),解可得f′(2)的值,即可得答案.
解答 解:根据题意,f(x)=3x2-2xf′(2),
则其导数f′(x)=6x-2f′(2),
令x=2可得:f′(2)=12-2f′(2),解可得f′(2)=4;
故答案为:4.
点评 本题考查导数的计算,注意f(x)=3x2-2xf′(2)中f′(2)为常数.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
17.复数z=(a+1)+(a2-3)i,若z<0,则实数a的值是( )
| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
20.已知函数f(x)=2x+x2-xln2-2,若函数g(x)=|f(x)|-loga(x+2)(a>1)在区间[-1,1]上有4个不同的零点,则实数a的取值范围是( )
| A. | (1,2) | B. | (2,+∞) | C. | [3${\;}^{\frac{1}{1-ln2}}$,+∞) | D. | (2,3${\;}^{\frac{1}{1-ln2}}$] |
10.在△ABC中,D在边BC上,且BD=2,DC=1,∠B=30°,∠ADC=150°,AB的长为$\frac{2\sqrt{3}}{3}$;△ABC的面积$\frac{\sqrt{3}}{2}$.
17.已知圆C的方程是x2+y2-6x+5=0,则圆C的圆心和半径分别为( )
| A. | (-3,0),2 | B. | (3,0),2 | C. | (-3,0),$\sqrt{2}$ | D. | (3,0),$\sqrt{2}$ |
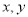 的值如下表所示,如果
的值如下表所示,如果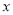 与
与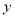 线性相关,且回归直线方程为
线性相关,且回归直线方程为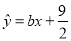 ,则实数
,则实数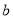 的值为( )
的值为( )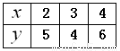
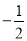 B.
B.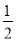 C.
C.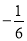 D.
D.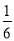
 ,则球O的表面积为 ( )
,则球O的表面积为 ( ) B.
B. C.
C. D.
D.