题目内容
2.若θ是任意实数,则方程x2+y2sinθ=4表示的曲线可能是①②④⑤.(填上所有可能的序号)①椭圆 ②双曲线 ③抛物线 ④圆 ⑤直线 ⑥点.
分析 根据sinθ的范围,可判断方程可表示圆,直线,双曲线,椭圆,故可得结论.
解答 解:由题意,sinθ∈[-1,1],
∴sinθ=1时,方程表示圆;sinθ=0时,方程表示两条直线;
sinθ∈[-1,0)时,方程表示双曲线;sinθ∈(0,1),方程表示椭圆.
故答案为:①②④⑤.
点评 本题以方程为载体,考查方程与曲线的关系,解题的关键是根据sinθ的范围,进行分类讨论,属于中档题.

练习册系列答案
相关题目
10.在△ABC中,D在边BC上,且BD=2,DC=1,∠B=30°,∠ADC=150°,AB的长为$\frac{2\sqrt{3}}{3}$;△ABC的面积$\frac{\sqrt{3}}{2}$.
17.已知圆C的方程是x2+y2-6x+5=0,则圆C的圆心和半径分别为( )
| A. | (-3,0),2 | B. | (3,0),2 | C. | (-3,0),$\sqrt{2}$ | D. | (3,0),$\sqrt{2}$ |
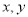 的值如下表所示,如果
的值如下表所示,如果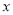 与
与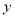 线性相关,且回归直线方程为
线性相关,且回归直线方程为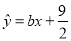 ,则实数
,则实数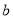 的值为( )
的值为( )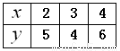
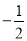 B.
B.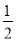 C.
C.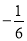 D.
D.