题目内容
15.设向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(3,1),则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为(4,3),$\overrightarrow{a}$•$\overrightarrow{b}$=5.分析 利用向量的坐标运算性质、数量积运算性质即可得出.
解答 解:$\overrightarrow{a}+\overrightarrow{b}$=(4,3),$\overrightarrow{a}•\overrightarrow{b}$=3+2=5.
故答案为:(4,3),5.
点评 本题考查了向量的坐标运算性质、数量积运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
7.$\overrightarrow{AB}$+$\overrightarrow{AC}$-$\overrightarrow{BC}$+$\overrightarrow{BA}$化简后等于( )
| A. | $\overrightarrow{AB}$ | B. | 3 $\overrightarrow{AB}$ | C. | $\overrightarrow{BA}$ | D. | $\overrightarrow{CA}$ |
10.在△ABC中,D在边BC上,且BD=2,DC=1,∠B=30°,∠ADC=150°,AB的长为$\frac{2\sqrt{3}}{3}$;△ABC的面积$\frac{\sqrt{3}}{2}$.
20.已知椭圆$\frac{x^2}{16}+\frac{y^2}{12+m}=1的离心率e=\frac{{\sqrt{2}}}{2}$实数m为( )
| A. | -4或16 | B. | 20 | C. | -4或20 | D. | -4 |
7.设正实数x,y满足x>$\frac{1}{2}$,y>1,不等式$\frac{4{x}^{2}}{y-1}$+$\frac{{y}^{2}}{2x-1}$≥m恒成立,则m的最大值为( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 8 | D. | 16 |
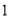 、
、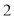 、
、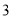 、
、 、
、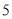 、
、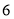 个点)两次,落在水平桌面后,记正面朝上的点数分别为
个点)两次,落在水平桌面后,记正面朝上的点数分别为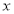 ,
,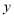 ,设事件
,设事件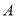 为“
为“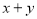 为偶数”, 事件
为偶数”, 事件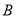 为 “
为 “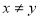 ”,则概率
”,则概率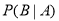 等于_________.
等于_________.