题目内容
1.已知在△ABC中,角A、B、C的对边分别为a,b,c,且cosC=-$\frac{1}{4}$,c=4,$\frac{sinA}{sinB}$=$\frac{2}{3}$(I)求a,b的值以及△ABC的面积;
(Ⅱ)记AD为A的角平分线且交BC 于D,求AD的值.
分析 (Ⅰ)由正弦、余弦定理列出方程组,求出b和a的值,再计算△ABC的面积;
(Ⅱ)根据角平分线定理求得CD的值,再由余弦定理求得AD的值.
解答 解:(Ⅰ)△ABC中,cosC=-$\frac{1}{4}$,c=4,$\frac{sinA}{sinB}$=$\frac{2}{3}$,
由正弦定理得$\frac{a}{b}$=$\frac{2}{3}$,∴a=$\frac{2}{3}$b;
由余弦定理得c2=a2+b2-2abcosC
=$\frac{4}{9}$b2+b2-2×$\frac{2}{3}$b×b×(-$\frac{1}{4}$)
=$\frac{16}{9}$b2=16,
解得b=3,∴a=2;
∴△ABC的面积为
S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}$×2×3×$\sqrt{1{-(-\frac{1}{4})}^{2}}$=$\frac{3\sqrt{15}}{4}$;
(Ⅱ)如图所示,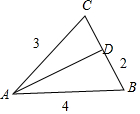
根据角平分线定理得,$\frac{CD}{BD}$=$\frac{AC}{AB}$=$\frac{3}{4}$,
∴CD=BC×$\frac{3}{7}$=$\frac{6}{7}$;
由余弦定理得AD2=AC2+CD2-2AC•CD•cosC
=32+${(\frac{6}{7})}^{2}$-2×3×$\frac{6}{7}$×(-$\frac{1}{4}$)
=$\frac{540}{49}$,
∴AD=$\frac{6\sqrt{15}}{7}$.
点评 本题考查了正弦、余弦定理的应用问题,也考查了求三角形的面积以及角平分线长的应用问题,是综合题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
2.设{an}是公比负数的等比数列,a1=2,a3-4=a2,则a3=( )
| A. | 2 | B. | -2 | C. | 8 | D. | -8 |
6.将圆C:(x-1)2+y2=25按向量$\overrightarrow{a}$=(1,1)平移得到圆C′,则圆C′的圆心和半径分别为( )
| A. | (1,0),5 | B. | (0,1),5 | C. | (-1,0),5 | D. | (2,1),5 |
10.函数f(x)的定义域为R,若f(x+1)与f(x-1)都是奇函数,则f(5)=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 5 |
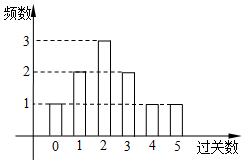 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.