题目内容
17.已知数列{an}是公比为2的等比数列,且a2,a3+1,a4成等差数列.( I)求数列{an}的通项公式;
( II)记bn=an+log2an+1,求数列{bn}的前n项和Tn.
分析 ( I )由题意可得2(a3+1)=a2+a4,由公比为2,把a3、a4用a2表示,求得a2,进一步求出a1,数列{an}的通项公式.
(Ⅱ)利用已知条件转化求出数列的通项公式,然后求解数列的和即可.
解答 解:(Ⅰ)由题意可得2(a3+1)=a2+a4,
即2(2a2+1)=a2+4a2,解得:a2=2.
∴a1=$\frac{{a}_{2}}{2}$=1.
∴数列{an}的通项公式为an=2n-1.
(Ⅱ)bn=an+log2an+1=2n-1+n,
Tn=b1+b2+b3+…+bn=(1+2+3+…+n)+(20+21+22+…+2n-1)
=$\frac{n(n+1)}{2}+\frac{1-{2}^{n}}{1-2}$
=$\frac{n(n+1)}{2}+{2}^{n}-1$.
点评 本题考查等差数列和等比数列的通项公式,考查了等比数列的前n项和,是基础的计算题.

练习册系列答案
相关题目
7.执行如图所示的程序框图,如图输出S的值为-1,那么判断框内应填入的条件是( )
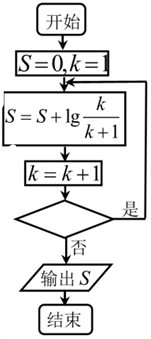

| A. | k≤8 | B. | k≤9 | C. | k≤10 | D. | k≤11 |
8.已知f(x)=$\left\{\begin{array}{l}{-2{x}^{2}+3x,-2≤x<0}\\{ln\frac{1}{x+1},0≤x≤2}\end{array}\right.$,若g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则实数a的取值范围为( )
| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | C. | (0,$\frac{1}{e}$) | D. | (0,$\frac{1}{2e}$) |
5.△ABC中,角A、B、C的对边分别为a、b、c,G是平面△ABC上一点,且满足a•$\overrightarrow{GA}$+b•$\overrightarrow{GB}$+c•$\overrightarrow{GC}$=0,则G是△ABC中的( )
| A. | 内心 | B. | 外心 | C. | 重心 | D. | 垂心 |
6.设x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$,目标函数z=ax+by(a>0,b>0)的最大值为M,若M的取值范围是[1,2],则点M(a,b)所经过的区域面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
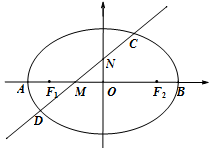 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.