题目内容
13.设x,y∈R,向量$\overrightarrow a=({x,2})$,$\overrightarrow b=({1,y})$,$\overrightarrow c=({2,-6})$,且$\overrightarrow a⊥\overrightarrow c$,$\overrightarrow b∥\overrightarrow c$,则$|{\overrightarrow a+\overrightarrow b}|$=$5\sqrt{2}$.分析 根据题意,若$\overrightarrow a⊥\overrightarrow c$,由向量垂直的判定方法可得2x+2×(-6)=0,解可得x的值,即可得$\overrightarrow{a}$的坐标,若$\overrightarrow b∥\overrightarrow c$,由向量平行的坐标表示公式可得2y=1×(-6),解可得y的值,即可得$\overrightarrow{b}$的坐标,由向量加法的坐标计算公式可得$\overrightarrow{a}$+$\overrightarrow{b}$的坐标,由向量模的计算公式计算可得答案.
解答 解:根据题意,向量$\overrightarrow a=({x,2})$,$\overrightarrow b=({1,y})$,$\overrightarrow c=({2,-6})$,
若$\overrightarrow a⊥\overrightarrow c$,则有2x+2×(-6)=0,解可得x=6,即$\overrightarrow{a}$=(6,2),
若$\overrightarrow b∥\overrightarrow c$,则有2y=1×(-6),解可得y=-3,即$\overrightarrow{b}$=(1,-3),
则$\overrightarrow{a}$+$\overrightarrow{b}$=(7,-1),
则$|{\overrightarrow a+\overrightarrow b}|$=$\sqrt{49+1}$=$5\sqrt{2}$;
故答案为:5$\sqrt{2}$.
点评 本题考查向量的数量积的计算,关键是求出$\overrightarrow{a}$、$\overrightarrow{b}$的坐标.

| A. | -i | B. | i | C. | 2i | D. | -2i |
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 1或2 |
| 买房 | 不买房 | 纠结 | |
| 城市人 | 5 | 15 | |
| 农村人 | 20 | 10 |
(1)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(2)用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$.
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| A. | ±4 | B. | -4 | C. | 4 | D. | 5 |
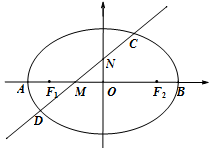 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.