题目内容
18.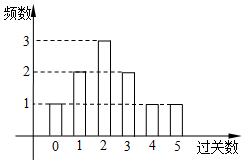 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.(Ⅰ)求小明在这十次游戏中所得奖品数的均值;
(Ⅱ)规定过三关者才能玩另一个高级别的游戏,估计小明一次游戏后能玩另一个游戏的概率;
(Ⅲ)已知小明在某四次游戏中所过关数为{2,2,3,4},小聪在某四次游戏中所过关数为{3,3,4,5},现从中各选一次游戏,求小明和小聪所得奖品总数超过10的概率.
分析 (Ⅰ)列出小明的过关数与奖品数对应表,由此能求出小明在这十次游戏中所得奖品数的均值.
(Ⅱ)利用等可能事件概率计算公式能求出小明一次游戏后能玩另一个游戏的概率.
(Ⅲ)小明在四次游戏中所得奖品数为{2,2,4,8},小聪在四次游戏中所得奖品数为{4,4,8,16},由此利用列举法能求出小明和小聪所得奖品总数超过10的概率.
解答 解:(Ⅰ)小明的过关数与奖品数如下表:
| 过关数 | 0 | 1 | 2 | 3 | 4 | 5 |
| 奖品数 | 0 | 1 | 2 | 4 | 8 | 16 |
小明在这十次游戏中所得奖品数的均值为:
$\frac{1}{10}(1×2+2×3+4×2+8×1+16×1)=4$;------------------------------------(4分)
(Ⅱ)小明一次游戏后能玩另一个游戏的概率约为$\frac{2+1+1}{10}=0.4$;---------------(6分)
(Ⅲ)小明在四次游戏中所得奖品数为{2,2,4,8},--------------------------------------(7分)
小聪在四次游戏中所得奖品数为{4,4,8,16},-------------------------------------(8分)
现从中各选一次游戏,奖品总数如下表:
| 2 | 2 | 4 | 8 | |
| 4 | 6 | 6 | 8 | 12 |
| 4 | 6 | 6 | 8 | 12 |
| 8 | 10 | 10 | 12 | 16 |
| 16 | 18 | 18 | 20 | 24 |
共16个基本事件,总数超过10的有8个基本事件,故所求的概率为$\frac{8}{16}=\frac{1}{2}$.----(12分)
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
8.已知f(x)=$\left\{\begin{array}{l}{-2{x}^{2}+3x,-2≤x<0}\\{ln\frac{1}{x+1},0≤x≤2}\end{array}\right.$,若g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则实数a的取值范围为( )
| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | C. | (0,$\frac{1}{e}$) | D. | (0,$\frac{1}{2e}$) |
6.设x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$,目标函数z=ax+by(a>0,b>0)的最大值为M,若M的取值范围是[1,2],则点M(a,b)所经过的区域面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
13.如图是一个算法流程图,则输出的x值为( )


| A. | 95 | B. | 47 | C. | 23 | D. | 11 |
3.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的一条渐近线方程为2x+y=0,则C的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$或$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
10.已知i为虚数单位,z(1-i)=1+i,则复数z的共轭复数为( )
| A. | -i | B. | i | C. | 2i | D. | -2i |
2.复数z满足$({1-\sqrt{3}i})z=i$(S为虚数单位),则|z|=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
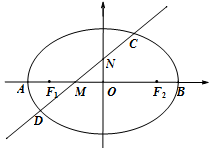 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.