题目内容
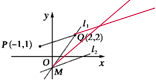
已知P(-1,1)、Q(2,2),若直线l:x+my+m=0与线段PQ的延长线相交,则m的取值范围是 .
考点:直线的图象特征与倾斜角、斜率的关系
专题:直线与圆
分析:先求出PQ的斜率,再分情况讨论出直线的几种特殊情况,综合即可得到答案.
解答:
 解:由题知kPQ=
解:由题知kPQ=
=
,
直线x+my+m=0过点M(0,-1).
当m=0时,直线化为x=0,一定与PQ相交,所以m≠0,
当m≠0时,k1=-
,考虑直线l的两个极限位置.
(1)l经过Q,即直线l1,则kl1=
=
;
(2)l与
平行,即直线l2,则kl2=kPQ=
,
所以
<-
<
,
即-3<m<-
.
故答案为:-3<m<-
 解:由题知kPQ=
解:由题知kPQ=| 2-1 |
| 2-(-1) |
| 1 |
| 3 |
直线x+my+m=0过点M(0,-1).
当m=0时,直线化为x=0,一定与PQ相交,所以m≠0,
当m≠0时,k1=-
| 1 |
| m |
(1)l经过Q,即直线l1,则kl1=
| 2-(-1) |
| 2-0 |
| 3 |
| 2 |
(2)l与
| PQ |
| 1 |
| 3 |
所以
| 1 |
| 3 |
| 1 |
| m |
| 3 |
| 2 |
即-3<m<-
| 2 |
| 3 |
故答案为:-3<m<-
| 2 |
| 3 |
点评:本题主要是考查平面向量以及直线之间的位置关系的综合题.其中涉及到分类讨论思想的应用,属于基础题目.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
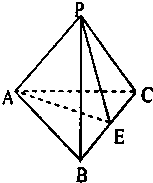 如图所示,点P是平面ABC外一点,且满足PA、PB、PC两两垂直,PE⊥BC,则该图中两两垂直的平面共有( )
如图所示,点P是平面ABC外一点,且满足PA、PB、PC两两垂直,PE⊥BC,则该图中两两垂直的平面共有( )| A、3对 | B、4对 | C、5对 | D、6对 |
极坐标平面内,集合P={(ρ,θ)|sinθ=-
,ρ∈R}与集合S={(ρ,θ)|cosθ=
,ρ∈R}之间的关系是( )
| 1 |
| 2 |
| ||
| 2 |
| A、P?S |
| B、P?S |
| C、P=S |
| D、P∩S={(0,0)} |
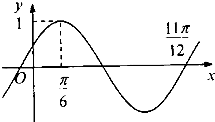 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ| 如图所示,一个空间几何的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为
如图所示,一个空间几何的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为