题目内容
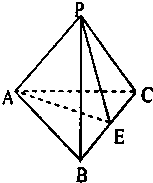如图所示，点P是平面ABC外一点，且满足PA、PB、PC两两垂直，PE⊥BC，则该图中两两垂直的平面共有（ ）| A、3对 | B、4对 | C、5对 | D、6对 |
考点：平面与平面垂直的判定
专题：证明题,空间位置关系与距离
分析：利用线面、面面垂直的判定定理可得结论．
解答：
解：∵点P是平面ABC外一点，且满足PA、PB、PC两两垂直，
∴平面PAB与平面PBC，平面PAB与平面PAC；平面PBC与平面PAC互相垂直．
∵PE⊥BC，
∴平面PAE⊥平面PBC，
∴图中两两垂直的平面共有4对．
故选：B．
∴平面PAB与平面PBC，平面PAB与平面PAC；平面PBC与平面PAC互相垂直．
∵PE⊥BC，
∴平面PAE⊥平面PBC，
∴图中两两垂直的平面共有4对．
故选：B．
点评：本题考查线面、面面垂直的判定定理，比较基础．
练习册系列答案
53随堂测系列答案
相关题目
函数y=-|x|（x∈[-2，2]）的图象是（ ）
A、 |
B、 |
C、 |
D、 |
下列命题中正确的是（ ）
| A、空间中的任意三点确定一个平面 |
| B、空间中两两相交的三条直线确定一个平面 |
| C、有且只有一组对边平行的四边形是平面图形 |
| D、两组对边分别相等的四边形一定是平面图形 |
函数f（x）的导函数f′（x）=2x+2，则f（x）可能是（ ）
| A、f（x）=x2+2 |
| B、f（x）=2x+2 |
| C、f（x）=x2+2x-3 |
| D、f（x）=x3+x2 |
已知x=
与x=
为函数f（x）=3sin（ωx+
）的两条相邻对称轴，则ω=（ ）
| π |
| 4 |
| 3π |
| 4 |
| π |
| 6 |
| A、1 | B、2 | C、±1 | D、±2 |