Question

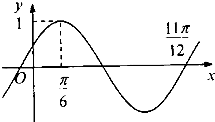函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

π

2

）的部分图象如图所示，则函数y=f（x）对应的解析式为

 

．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由y=Asin（ωx+φ）的部分图象可求得A=1，T=π，从而可得ω，再由f（

π

6

）=sin（2×

π

6

+φ）=1，|φ|＜

π

2

可求得φ，从而可得答案．

解答： 解：∵

3

4

T=

3

4

•

2π

ω

=

11π

12

-

π

6

=

3π

4

，
∴ω=2；
又A=1，f（

π

6

）=sin（2×

π

6

+φ）=1，
∴

π

3

+φ=kπ+

π

2

，k∈Z．
∴φ=kπ+

π

6

（k∈Z），又|φ|＜

π

2

，
∴φ=

π

6

，
∴f（x）=sin（2x+

π

6

）．
故答案为：f（x）=sin（2x+

π

6

）．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定函数解析式，求得φ的值是难点，属于中档题．