题目内容

9．若$P（ξ=K）=\frac{1}{2^K}$，则$\frac{n!}{{3!（{n-3}）!}}$的值为（　　）
A．1B．20C．35D．7

分析 根据$P（ξ=K）=\frac{1}{2^K}$，求出n，即可求出$\frac{n!}{{3!（{n-3}）!}}$的值．

解答 解：由$P（ξ=K）=\frac{1}{2^K}$，得$\frac{n（n-1）（n-2）}{3×2×1}=\frac{n（n-1）（n-2）（n-3）}{4×3×2×1}，n=7$，
所以$\frac{n!}{{3!（{n-3}）!}}=\frac{7×6×5×4!}{3!4!}=\frac{7×6×5}{3×2×1}=35$．
故选C．

点评 本题考查二项分布，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
15．已知点A（4，4）在抛物线y2=2px （p＞0）上，该抛物线的焦点为F，过点A作该抛物线准线的垂线，垂足为E，则∠EAF的平分线所在的直线方程为（　　）
A．2x+y-12=0B．x+2y-12=0C．2x-y-4=0D．x-2y+4=0
20．若x，y满足约束条件$\left\{\begin{array}{l}x+y-5≤0\\ 2x-y-1≥0\\ x-2y+1≤0\end{array}\right.$，则z=x+y的最大值为5．
17．已知函数$f（x）=\left\{\begin{array}{l}kx-k（x≥0）\\{x^2}+2ax-{（{a-2}）^2}（x＜0）\end{array}\right.$，其中a∈R，若对任意的非零实数x1，存在唯一的非零实数x2（x2≠x1），使得f（x2）=f（x1）成立，则k的最小值为（　　）
A．1B．2C．3D．4
4．已知直线l：y=k（x-1）交x轴于点A，交y轴于点B，交直线y=x于点C，
（1）若k=3，求$\frac{{|{BC}|}}{{|{AC}|}}$的值；
（2）若|BC|=2|AC|，求直线l的方程．
14．谷志伟，简书两位老师下棋，简老师获胜的概率是40%，谷老师不胜的概率为60%，则两位老师下成和棋的概率为（　　）
A．10%B．30%C．20%D．50%
1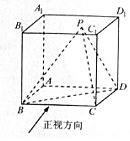．如图，在正方体ABC的-A1B1C1D1中，点P是线段A1C1上的动点，则三棱锥P-BCD的俯视图与正视图面积之比的最大值为（　　）
A．1B．$\sqrt{2}$C．$\sqrt{3}$D．2
18．若复数z满足（3-4i+z）i=2+i，则复数z所对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
19．已知a＞2，b＞2，直线$y=-\frac{b}{a}x+b$与曲线（x-1）2+（y-1）2=1只有一个公共点，则ab的取值范围为（　　）
A．$（4，6+4\sqrt{2}）$B．$（4，6+4\sqrt{2}]$C．$[6+4\sqrt{2}，+∞）$D．$（6+4\sqrt{2}，+∞）$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网