题目内容
1．
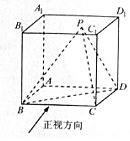如图，在正方体ABC的-A1B1C1D1中，点P是线段A1C1上的动点，则三棱锥P-BCD的俯视图与正视图面积之比的最大值为（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
分析 分析三棱锥P-BCD的正视图与侧视图的形状，并求出面积，可得答案．
解答 解：设棱长为1，则三棱锥P-BCD的正视图是底面边长为1，高为1的三角形，面积为：$\frac{1}{2}$；
三棱锥P-BCD的俯视图取最大面积时，P在A1处，是个正方形，俯视图面积为：1；
故三棱锥P-BCD的俯视图与正视图面积之比的最大值为2，
故选：D．
点评 本题考查的知识点是简单空间图形的三视图，根据已知分析出三棱锥P-BCD的正视图与侧视图的形状，是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
12．关于不同的直线m，n与不同的平面α，β，有下列四个命题：
①m⊥α，n⊥β且α⊥β，则m⊥n；②m∥α，n∥β且α∥β，则m∥n；
③m⊥α，n∥β且α∥β，则m⊥n； ④m∥α，n⊥β且α⊥β，则m∥n．
其中正确的命题的序号是（ ）
①m⊥α，n⊥β且α⊥β，则m⊥n；②m∥α，n∥β且α∥β，则m∥n；
③m⊥α，n∥β且α∥β，则m⊥n； ④m∥α，n⊥β且α⊥β，则m∥n．
其中正确的命题的序号是（ ）
| A． | ①② | B． | ②③ | C． | ①③ | D． | ②④ |
16．设a，b，c＞0，则$a+\frac{1}{b}，b+\frac{1}{c}，c+\frac{1}{a}$（ ）
| A． | 都不大于2 | B． | 都不小于2 | ||
| C． | 至少有一个不大于2 | D． | 至少有一个不小于2 |
13．在△ABC中，AH⊥BC于H，点D满足$\overrightarrow{BD}$=2$\overrightarrow{DC}$，若|$\overrightarrow{AH}$|=$\sqrt{2}$，则$\overrightarrow{AH}$•$\overrightarrow{AD}$=（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | 2$\sqrt{2}$ | D． | 4 |
10．已知集合M={0，2，zi}，i为虚数单位，N={1，3}，M∩N={1}，则复数z=（ ）
| A． | -i | B． | i | C． | -2i | D． | 2i |