题目内容
4.已知直线l:y=k(x-1)交x轴于点A,交y轴于点B,交直线y=x于点C,(1)若k=3,求$\frac{{|{BC}|}}{{|{AC}|}}$的值;
(2)若|BC|=2|AC|,求直线l的方程.
分析 (1)求出A,B,C的坐标,即可求$\frac{{|{BC}|}}{{|{AC}|}}$的值;
(2)直线l的方程为y=k(x-1),若|BC|=2|AC|,则|xB-xC|=2|xA-xC|,求出k,即可求直线l的方程.
解答 解:(1)直线l的方程为y=3(x-1).
令y=0,得A(1,0).…(1分),令x=0,得B(0,-3).…(2分)
由$\left\{\begin{array}{l}y=x\\ y=3({x-1})\end{array}\right.$得${x_C}=\frac{3}{2}$…(3分)
$\frac{{|{BC}|}}{{|{AC}|}}=\frac{{|{{x_B}-{x_C}}|}}{{|{{x_A}-{x_C}}|}}=\frac{{|{\frac{3}{2}}|}}{{|{\frac{1}{2}}|}}=3$…(5分)
(2)直线l的方程为y=k(x-1).
令y=0,得A(1,0).令x=0,得B(0,-k).…(6分)
由$\left\{\begin{array}{l}y=x\\ y=k({x-1})\end{array}\right.$得${x_C}=\frac{k}{k-1}$…(7分)
若|BC|=2|AC|,则|xB-xC|=2|xA-xC|…(8分)
∴$|{\frac{k}{k-1}}|=2|{1-\frac{k}{k-1}}|$…(9分)
∴解得k=±2…(11分)
∴所求直线l的方程为:2x-y-2=0或2x+y-2=0.…(12分)
点评 本题考查直线方程,考查直线与直线位置关系的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
15.已知函数f(x)=x2-mx-m2,则f(x)( )
| A. | 有一个零点 | B. | 有两个零点 | ||
| C. | 有一个或两个零点 | D. | 无零点 |
12.关于不同的直线m,n与不同的平面α,β,有下列四个命题:
①m⊥α,n⊥β且α⊥β,则m⊥n;②m∥α,n∥β且α∥β,则m∥n;
③m⊥α,n∥β且α∥β,则m⊥n; ④m∥α,n⊥β且α⊥β,则m∥n.
其中正确的命题的序号是( )
①m⊥α,n⊥β且α⊥β,则m⊥n;②m∥α,n∥β且α∥β,则m∥n;
③m⊥α,n∥β且α∥β,则m⊥n; ④m∥α,n⊥β且α⊥β,则m∥n.
其中正确的命题的序号是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
16.设a,b,c>0,则$a+\frac{1}{b},b+\frac{1}{c},c+\frac{1}{a}$( )
| A. | 都不大于2 | B. | 都不小于2 | ||
| C. | 至少有一个不大于2 | D. | 至少有一个不小于2 |
13.在△ABC中,AH⊥BC于H,点D满足$\overrightarrow{BD}$=2$\overrightarrow{DC}$,若|$\overrightarrow{AH}$|=$\sqrt{2}$,则$\overrightarrow{AH}$•$\overrightarrow{AD}$=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
14.设a=sin$\frac{π}{5}$,b=log${\;}_{\sqrt{2}}$$\sqrt{3}$,c=($\frac{1}{4}$)${\;}^{\frac{2}{3}}$,则( )
| A. | a<c<b | B. | b<a<c | C. | c<a<b | D. | c<b<a |
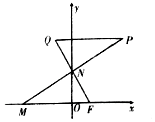 已知点F(1,0),动点M,N分别在x轴,y轴上运动,MN⊥NF,Q为平面上一点,$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$,过点Q作QP平行于x轴交MN的延长线于点P.
已知点F(1,0),动点M,N分别在x轴,y轴上运动,MN⊥NF,Q为平面上一点,$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$,过点Q作QP平行于x轴交MN的延长线于点P.