题目内容
18.若复数z满足(3-4i+z)i=2+i,则复数z所对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 把已知等式变形,利用复数代数形式的乘除运算化简求得z,得到z的坐标得答案.
解答 解:由(3-4i+z)i=2+i,得
3-4i+z=$\frac{2+i}{i}=\frac{(2+i)(-i)}{-{i}^{2}}=1-2i$,
∴z=-2+2i.
∴复数z所对应的点的坐标为(-2,2),位于第二象限.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
13.在△ABC中,AH⊥BC于H,点D满足$\overrightarrow{BD}$=2$\overrightarrow{DC}$,若|$\overrightarrow{AH}$|=$\sqrt{2}$,则$\overrightarrow{AH}$•$\overrightarrow{AD}$=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
3.已知圆的方程是x2+y2=1,则经过圆上一点M(1,0)的切线方程是( )
| A. | x=1 | B. | y=1 | C. | x+y=1 | D. | x-y=1 |
10.已知集合M={0,2,zi},i为虚数单位,N={1,3},M∩N={1},则复数z=( )
| A. | -i | B. | i | C. | -2i | D. | 2i |
8.已知圆C1:x2+y2=4,圆C2:x2+y2+6x-8y+16=0,则圆C1和圆C2的位置关系是( )
| A. | 相离 | B. | 外切 | C. | 相交 | D. | 内切 |
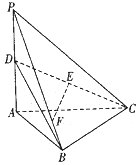 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}$=3$\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}$=3$\overrightarrow{FB}$.