题目内容
20.在△ABC中,AB=2,AC=1,∠A=$\frac{2π}{3}$,过A作AD⊥BC于D,且$\overrightarrow{AD}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λμ=( )| A. | $\frac{10}{49}$ | B. | $\frac{5\sqrt{7}}{14}$ | C. | $\frac{9}{7}$ | D. | 1 |
分析 根据余弦定理解出BC,根据等面积法求出AD,使用勾股定理求出CD,得出$\overrightarrow{CD},\overrightarrow{CB}$的数量关系,用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AD}$得到λ,μ的值.
解答  解:在△ABC中,由余弦定理得BC=$\sqrt{A{B}^{2}+A{C}^{2}-2AB•ACcos120°}$=$\sqrt{7}$.
解:在△ABC中,由余弦定理得BC=$\sqrt{A{B}^{2}+A{C}^{2}-2AB•ACcos120°}$=$\sqrt{7}$.
∵S△ABC=$\frac{1}{2}AB•AC•sin\frac{2π}{3}$=$\frac{1}{2}AC•AD$,∴AD=$\frac{\sqrt{21}}{7}$.
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\frac{2\sqrt{7}}{7}$.
∴$\overrightarrow{CD}=\frac{2}{7}\overrightarrow{CB}$=$\frac{2}{7}$($\overrightarrow{AB}-\overrightarrow{AC}$).∴$\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{CD}$=$\frac{2}{7}\overrightarrow{AB}+\frac{5}{7}\overrightarrow{AC}$.
∴λ=$\frac{2}{7}$,$μ=\frac{5}{7}$.
∴λμ=$\frac{10}{49}$.
故选:A.
点评 本题考查了平面向量的线性运算的几何意义,属于中档题.

练习册系列答案
相关题目
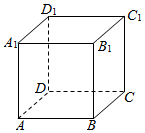 如图,正方体ABCD-A1B1C1D1的棱长为1,请在此正方体中取出四个顶点构成一个三棱锥,满足三棱锥的四个面都是直角三角形,并求此三棱锥的体积.
如图,正方体ABCD-A1B1C1D1的棱长为1,请在此正方体中取出四个顶点构成一个三棱锥,满足三棱锥的四个面都是直角三角形,并求此三棱锥的体积. 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图: