题目内容
9．
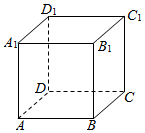如图，正方体ABCD-A1B1C1D1的棱长为1，请在此正方体中取出四个顶点构成一个三棱锥，满足三棱锥的四个面都是直角三角形，并求此三棱锥的体积．
分析 由正方体的结构特征可知以B，C，D，B1为顶点的四边形符合条件．
解答 解：连结BD，B1，B1C，则三棱锥B1-BCD即为符合条件的一个三棱锥
三棱锥的体积V=$\frac{1}{3}{S}_{△BCD}•B{B}_{1}$=$\frac{1}{3}×\frac{1}{2}×{1}^{2}×1=\frac{1}{6}$．
点评 本题考查了正方体的结构特征，棱锥的体积计算，属于基础题．
练习册系列答案
相关题目
20．在△ABC中，AB=2，AC=1，∠A=$\frac{2π}{3}$，过A作AD⊥BC于D，且$\overrightarrow{AD}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$，则λμ=（ ）
| A． | $\frac{10}{49}$ | B． | $\frac{5\sqrt{7}}{14}$ | C． | $\frac{9}{7}$ | D． | 1 |
17．函数y=2sin（ωx+φ）是偶函数，则φ可能等于（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | π |
4．如图，网格纸上小正方形的边长为1，粗实线画出的是某三棱锥的三视图，则该三棱锥的体积为（ ）
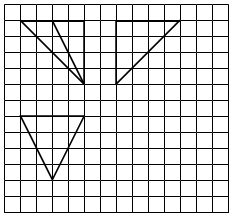
| A． | $\frac{16}{3}$ | B． | $\frac{{16\sqrt{3}}}{3}$ | C． | $\frac{32}{3}$ | D． | $\frac{64}{3}$ |
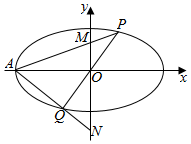已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$离心率$e=\frac{{\sqrt{3}}}{2}$，短轴长为2．
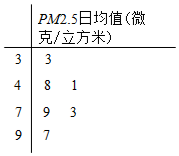PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．我国PM2.5标准采用世卫组织设定的最宽限值，PM2.5日均值在35微克/立方米以下空气质量为1级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米及其以上空气质量为超标．
18．在等比数列{an}中，已知a4=27a3，则$\frac{{a}_{2}}{{a}_{1}}$+$\frac{{a}_{4}}{{a}_{2}}$+$\frac{{a}_{6}}{{a}_{3}}$+…+$\frac{{a}_{2n}}{{a}_{n}}$等于（ ）
| A． | $\frac{{3}^{-n}-3}{2}$ | B． | $\frac{{3}^{1-n}-3}{2}$ | C． | $\frac{{3}^{n}-3}{2}$ | D． | $\frac{{3}^{n+1}-3}{2}$ |
19．已知函数f（x）定义域为R，则命题p：“函数f（x）为偶函数”是命题q：“?x0∈R，f（x0）=f（-x0）”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |