题目内容
5.已知向量|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=5,当(1)$\overrightarrow{a}$∥$\overrightarrow{b}$.
(2)$\overrightarrow{a}$⊥$\overrightarrow{b}$.
(3)$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为30°时,分别求$\overrightarrow{a}$与$\overrightarrow{b}$的数量积.
分析 根据平面向量的数量积定义计算.
解答 解:(1)当$\overrightarrow{a},\overrightarrow{b}$同向时,$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos0°=4×5=20;
当$\overrightarrow{a},\overrightarrow{b}$反向时,$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos180°=-4×5=-20.
(2)当$\overrightarrow{a}$⊥$\overrightarrow{b}$时,$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos90°=4×5×0=0.
(3)$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为30°时,$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos30°=4×5×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.在△ABC中,AB=2,AC=1,∠A=$\frac{2π}{3}$,过A作AD⊥BC于D,且$\overrightarrow{AD}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λμ=( )
| A. | $\frac{10}{49}$ | B. | $\frac{5\sqrt{7}}{14}$ | C. | $\frac{9}{7}$ | D. | 1 |
17.函数y=2sin(ωx+φ)是偶函数,则φ可能等于( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | π |
15.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-3).若向量$\overrightarrow{c}$满足$\overrightarrow{c}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),且$\overrightarrow{b}$∥($\overrightarrow{a}$-$\overrightarrow{c}$),则$\overrightarrow{c}$=( )
| A. | $(\frac{7}{9},\frac{7}{3})$ | B. | $(-\frac{7}{9},\frac{7}{3})$ | C. | $(\frac{7}{9},-\frac{7}{3})$ | D. | $(-\frac{7}{9},-\frac{7}{3})$ |
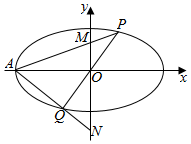 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$离心率$e=\frac{{\sqrt{3}}}{2}$,短轴长为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$离心率$e=\frac{{\sqrt{3}}}{2}$,短轴长为2.